
【题目】某工厂生产某种型号的电视机零配件,为了预测今年![]() 月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度
月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度![]() 月份至
月份至![]() 月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价
月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的
(单位:千件)之间的![]() 组数据如下表所示:
组数据如下表所示:
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
(1)根据1至![]() 月份的数据,求
月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(2)结合(1)中的线性回归方程,假设该型号电视机零配件的生产成本为每件![]() 元,那么工厂如何制定
元,那么工厂如何制定![]() 月份的销售单价,才能使该月利润达到最大(计算结果精确到
月份的销售单价,才能使该月利润达到最大(计算结果精确到![]() )?
)?
参考公式:回归直线方程![]() ,其中
,其中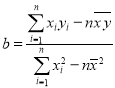 .
.
参考数据:![]() .
.
科目:高中数学 来源: 题型:
【题目】等差数列的定义可用数学符号语言描述为________,其中![]() ,其通项公式
,其通项公式![]() _________,
_________,![]() __________=_________,等差数列中,若
__________=_________,等差数列中,若![]() 则________(
则________(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为![]() 的函数
的函数![]() 满足:对于任意的实数
满足:对于任意的实数![]() 都有
都有![]() 成立,且当
成立,且当![]() 时,
时, ![]() 恒成立,且
恒成立,且![]() 是一个给定的正整数).
是一个给定的正整数).
(1)判断函数![]() 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(2)判断并证明![]() 的单调性;若函数
的单调性;若函数![]() 在
在![]() 上总有
上总有![]() 成立,试确定
成立,试确定![]() 应满足的条件;
应满足的条件;
(3)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设有5个条件类似的女孩(把她们分别记为A,B,C,D, E)应聘秘书工作,但只有2个秘书职位,因此5个人中只有2人能被录用.如果5个人被录用的机会相等,分别计算下列事件的概率;
(1)女孩A得到一个职位;
(2)女孩A和B各得到一个职位;
(3)女孩A或B得到一个职位.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,点P,G分别是
中,点P,G分别是![]() ,
,![]() 的中点,已知
的中点,已知![]() ⊥平面ABC,
⊥平面ABC,![]() =
=![]() =3,
=3,![]() =
=![]() =2.
=2.
(I)求异面直线![]() 与AB所成角的余弦值;
与AB所成角的余弦值;
(II)求证:![]() ⊥平面
⊥平面![]() ;
;
(III)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,上顶点为A,在x轴负半轴上有一点B,满足
,上顶点为A,在x轴负半轴上有一点B,满足![]() 为线段
为线段![]() 的中点,且AB⊥
的中点,且AB⊥![]() 。
。
(I)求椭圆C的离心率;
(II)若过A、B、![]() 三点的圆与直线
三点的圆与直线![]() :
:![]() 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(III)在(I)的条件下,过右焦点![]() 作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果l是空间中的一条直线,![]() 是空间中的一个平面,判断下列命题的真假.
是空间中的一个平面,判断下列命题的真假.
(1)l与![]() 要么相交,要么不相交;
要么相交,要么不相交;
(2)要么l在![]() 内,要么l在
内,要么l在![]() 外;
外;
(3)要么l与![]() 平行,要么l在
平行,要么l在![]() 内.
内.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com