
【题目】数列
(1)在等差数列{an}中,a6=10,S5=5,求该数列的第8项a8;
(2)在等比数列{bn}中,b1+b3=10,b4+b6= ![]() ,求该数列的前5项和S5 .
,求该数列的前5项和S5 .
【答案】
(1)解:设数列{an}的公差为d,由已知a6=10,S5=5,
得 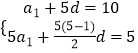 ,
,
解得 ![]() ,
,
所以a8=a1+7d=﹣5+7×3=16.
(或者a8=a6+2d=10+2×3=16)
(2)解:解法一:设数列{bn}的公比为q,由已知 ![]() ,
,
得 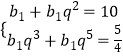 ,
,
解得 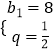 ,
,
所以 ![]() =
= 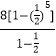 =
= ![]() .
.
解法二:设数列{bn}的公比为q.
由 ![]() ,得
,得 ![]() ,
,
从而得 ![]() .
.
又因为 ![]() ,
,
从而得b1=8.(9分)
所以 ![]() =
= 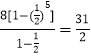 .
.
【解析】(1)由等差数列通项公式列出方程组,求出首项与公差,由此能求出该数列的第8项a8 . (2)法一:由等比数列通项公式列出方程组,求出首项与公比,由此能求出该数列的前5项和S5;法二:由 ![]() ,得
,得 ![]() ,从而求出公比,进而得b1 , 由此能求出该数列的前5项和S5 .
,从而求出公比,进而得b1 , 由此能求出该数列的前5项和S5 .
【考点精析】通过灵活运用等差数列的通项公式(及其变式)和等比数列的前n项和公式,掌握通项公式:![]() 或
或![]() ;前
;前![]() 项和公式:
项和公式: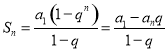 即可以解答此题.
即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】【2017福建三明5月质检】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)估计居民月均水量的中位数.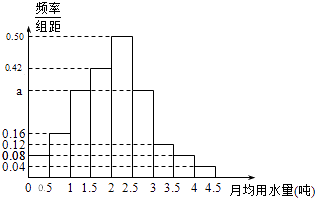
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强环保意识,我校从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
优秀 | 非优秀 | 总计 | |
男生 | 40 | 20 | 60 |
女生 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
(1)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(2)为参加市里举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为 ![]() ,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
附:K2= ![]()
P(K2≥k) | 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
k | 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,离心率 ![]() ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线 ![]() 的焦点重合.
的焦点重合.
(1)求椭圆C的方程;
(2)过点S( ![]() ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn=n2 , {bn}为等比数列,且a1=b1 , b2(a2﹣a1)=b1 .
(1)求数列{an},{bn}的通项公式.
(2)设cn=anbn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:直线y=kx+3与圆x2+y2=1相交于A,B两点;命题q:曲线![]() ﹣
﹣![]() =1表示焦点在y轴上的双曲线,若p∧q为真命题,求实数k的取值范围.
=1表示焦点在y轴上的双曲线,若p∧q为真命题,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+bx+c(其中b,c为实常数).
(1)若b>2,且y=f(sinx)(x∈R)的最大值为5,最小值为﹣1,求函数y=f(x)的解析式;
(2)是否存在这样的函数y=f(x),使得{y|y=x2+bx+c,﹣1≤x≤0}=[﹣1,0],若存在,求出函数y=f(x)的解析式;若不存在,请说明理由.
(3)记集合A={x|f(x)=x,x∈R},B={x|f(f(x))=x,x∈R}.
①若A≠,求证:B≠;
②若A=,判断B是否也为空集.
查看答案和解析>>
科目:高中数学 来源: 题型:
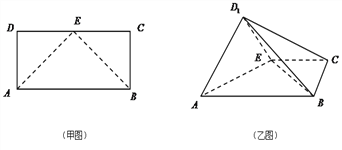
【题目】【2017四川宜宾二诊】如甲图所示,在矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起到
折起到![]() 位置,使平面
位置,使平面![]() 平面
平面![]() ,得到乙图所示的四棱锥
,得到乙图所示的四棱锥![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com