
【题目】某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图. 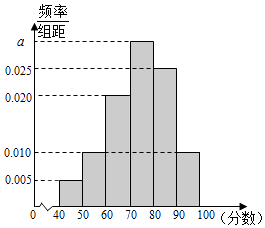
(1)求图中实数a的值;
(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
【答案】
(1)解:由于图中所有小矩形的面积之和等于1,
∴10×(0.005+0.01+0.02+a+0.025+0.01)=1.
解得a=0.03
(2)解:根据频率分布直方图,成绩不低于6(0分)的频率为
1﹣10×(0.005+0.01)=0.85.
由于该校高一年级共有学生640人,利用样本估计总体的思想,
可估计该校高一年级数学成绩不低于6(0分)的人数约为640×0.85=544人
(3)解:成绩在[40,50)分数段内的人数为40×0.05=2人,分别记为A,B.
成绩在[90,100]分数段内的人数为40×0.1=4人,分别记为C,D,E,F.(7分)
若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,
则所有的基本事件有:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),
(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.(9分)
如果两名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,
那么这两名学生的数学成绩之差的绝对值一定不大于10.
如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内,
那么这两名学生的数学成绩之差的绝对值一定大于10.
记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,
则事件M包含的基本事件有:
(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共7种.
所以所求概率为P(M)= ![]()
【解析】(1)根据阴影矩形的面积之和等于1,计算a的值;(2)首先计算成绩不低于60分的频率,即后四个小矩形的面积和,然后用640×频率计算人数;(3)若两名学生的学生成绩之差的绝对值不大于10,即两人是同一组的学生,那么首先计算两组的人数,并编号,并以编号的形式列出所有选取2人的基本事件的个数,同时计算同一组的两个人的所有基本事件的个数,最后相除得到概率.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知:以点 ![]() 为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为原点,
为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为原点,
(1)求证:△OAB的面积为定值;
(2)设直线y=﹣2x+4与圆C交于点M,N,若OM=ON,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直二面角D﹣AB﹣E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE. (Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求二面角B﹣AC﹣E的余弦值;
(Ⅲ)求点D到平面ACE的距离.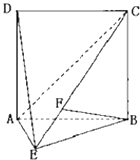
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把离心率e= ![]() 的双曲线
的双曲线 ![]() =1(a>0,b>0)称为黄金双曲线.如图是双曲线
=1(a>0,b>0)称为黄金双曲线.如图是双曲线 ![]() =1(a>0,b>0,c=
=1(a>0,b>0,c= ![]() )的图象,给出以下几个说法: ①若b2=ac,则该双曲线是黄金双曲线;
)的图象,给出以下几个说法: ①若b2=ac,则该双曲线是黄金双曲线;
②若F1 , F2为左右焦点,A1 , A2为左右顶点,B1(0,b),B2(0,﹣b)且∠F1B1A2=90°,则该双曲线是黄金双曲线;
③若MN经过右焦点F2且MN⊥F1F2 , ∠MON=90°,则该双曲线是黄金双曲线.
其中正确命题的序号为 . 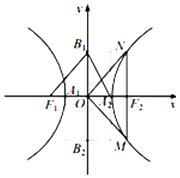
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 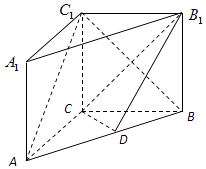
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求二面角B﹣DC﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)= ![]() x3+cx+3(c为常数),f(x)在x=0处的切线与直线y=x+2垂直.
x3+cx+3(c为常数),f(x)在x=0处的切线与直线y=x+2垂直.
(1)求函数y=f(x)的解析式;
(2)设g(x)=4lnx﹣f′(x),(其中f′(x)是函数f(x)的导函数),求g(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+1=0的圆心在直线ax﹣by+1=0上,则ab的取值范围是( )
A.(﹣∞, ![]() ]
]
B.(﹣∞, ![]() ]
]
C.(0, ![]() ]
]
D.(0, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com