练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若定义在上的函数满足，且是奇函数，现给出下列4个结论：①是周期为4的周期函数；

    ②的图象关于点对称；

    ③是偶函数；

    ④的图象经过点,其中正确结论的序号是__________（请填上所有正确的序号）．

    【答案】①②③

    【解析】

    求出函数f（x）的周期，判断出函数的奇偶性，从而求出答案即可．

    由f（x+2）=﹣f（x）可知函数周期为4，

    由f（x+1）是奇函数关于原点对称，

    可知f（x）关于（1，0）对称，即f（1+x）=﹣f（1﹣x），

    f（﹣x）=﹣f（﹣x+2）=﹣f（1+1﹣x）=f（1﹣（1﹣x））=f（x），

    所以函数为偶函数，f（﹣2）=﹣f（﹣2+2）=﹣f（0），无法判断其值．

    综上，正确的序号是：①②③．

    故答案为：①②③．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在等比数列中，．

    （Ⅰ）求数列的通项公式；

    （Ⅱ）若数列的公比大于，且，求数列的前项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】点A(0,2)是圆x2＋y2＝16内的定点，B，C是这个圆上的两个动点，若BA⊥CA，求BC中点M的轨迹方程，并说明它的轨迹是什么曲线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4﹣4：坐标系与参数方程．
    极坐标系与直角坐标系xoy有相同的长度单位，以原点为极点，以x轴正半轴为极轴，已知曲线C1的极坐标方程为ρ=4cosθ，曲线C2的参数方程为 （t为参数，0≤α＜π），射线θ=φ，θ=φ+ ，θ=φ﹣ 与曲线C1交于（不包括极点O）三点A、B、C．
    （1）求证：|OB|+|OC|= |OA|；
    （2）当φ= 时，B，C两点在曲线C2上，求m与α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在平行六面体ABCD-A1B1C1D1中,E,F,G分别是A1D1,D1D,D1C1的中点.

    (1)求证:EG∥AC;

    (2)求证:平面EFG∥平面AB1C.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知首项为﹣6的等差数列{an}的前7项和为0，等比数列{bn}满足b3=a7 ， |b3﹣b4|=6．
    （1）求数列{bn}的通项公式；
    （2）是否存在正整数k，使得数列{ }的前k项和大于 ？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x﹣1|+|3x﹣ |．
    （1）求不等式f（x）＜1的解集；
    （2）若实数a，b，c满足a＞0，b＞0，c＞0且a+b+c= ．求证： + + ≥ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在四棱锥A-BCDE中,底面BCDE是等腰梯形,BC∥ DE,∠ DCB=45°,O是BC中点,AO=,且BC=6,AD=AE=2CD=.

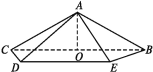
    (1)证明:AO⊥平面BCD;

    (2)求二面角A-CD-B的平面角的正切值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在正方体ABCD-A1B1C1D中，S是B1D1的中点，E、F、G分别是BC、CD和SC的中点．求证：

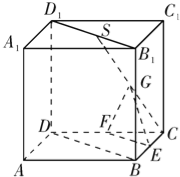
    （1）直线EG∥平面BDD1B1；

    （2）平面EFG∥平面BDD1B1．

    查看答案和解析>>

    同步练习册答案