
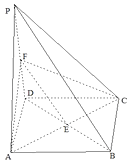
【题目】底面为正方形的四棱锥P﹣ABCD,F为PD中点. 
(1)求证:PB∥面ACF;
(2)若PD⊥面ABCD,求证:AC⊥面PBD.
【答案】
(1)证明:∵四边形ABCD为正方形,
∴E为BD中点.
∵F为棱PD中点.
∴PB∥EF.
∵PB平面ACF,EF平面ACF,
∴直线PB∥平面ACF
(2)解:∵PD⊥面ABCD,AC平面ABCD,
∴PD⊥AC,
又∵正方形ABCD中,有AC⊥BD,且PD∩BD=D,
∴AC⊥面PBD.
【解析】(1)根据线面平行的判定定理证明PB∥EF即可证明PB∥平面EAC;(2)由PD⊥面ABCD,可证PD⊥AC,又可证AC⊥BD,利用线面垂直的判定定理即可证明AC⊥面PBD.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】某学校为了解该校教师对教工食堂的满意度情况,随机访问了![]() 名教师.根据这
名教师.根据这![]() 名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:
名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为: ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() .
.
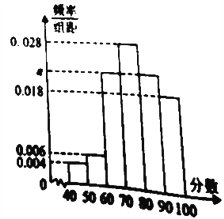
(1)求频率分布直方图中![]() 的值;
的值;
(2)从评分在![]() 的受访教师中,随机抽取2人,求此2人的评分都在
的受访教师中,随机抽取2人,求此2人的评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式an=5﹣n,其前n项和为Sn , 将数列{an}的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{bn}的前3项,记{bn}的前n项和为Tn , 若存在m∈N* , 使对任意n∈N* , 总有Sn<Tn+λ恒成立,则实数λ的取值范围是( )
A.λ≥2
B.λ>3
C.λ≥3
D.λ>2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据市场分析,某蔬菜加工点,当月产量为10吨至25吨时,月生产总成本![]() (万元)可以看出月产量
(万元)可以看出月产量![]() (吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.
(吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.
(I)写出月生产总成本![]() (万元)关于月产量
(万元)关于月产量![]() 吨的函数关系;
吨的函数关系;
(II)已知该产品销售价为每吨1.6万元,那么月产量为多少吨时,可获得最大利润,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点C在椭圆M: ![]() =1(a>b>0)上,若点A(﹣a,0),B(0,
=1(a>b>0)上,若点A(﹣a,0),B(0, ![]() ),且
),且 ![]() =
= ![]()
![]() .
.
(1)求椭圆M的离心率;
(2)设椭圆M的焦距为4,P,Q是椭圆M上不同的两点.线段PQ的垂直平分线为直线l,且直线l不与y轴重合.
①若点P(﹣3,0),直线l过点(0,﹣ ![]() ),求直线l的方程;
),求直线l的方程;
②若直线l过点(0,﹣1),且与x轴的交点为D.求D点横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com