练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】同学们有没有读过莎士比亚的名剧《威尼斯商人》？数学家斯摩林在剧中增加了一个情节：安东尼奥到鲍西娅家向她求婚，鲍西娅拿出一金、一银、一铝三个盒子，说：“每只盒子上写了一句话，但只有一句是真的.谁能猜中我的肖象在哪只盒子中，才能做我的丈夫”.如果你是聪明、政治的安东尼奥，请问肖象在哪个盒子内？（请从金盒、银盒、铝盒中选择一个填在横线上）________.

    【答案】银盒

    【解析】

    采用假设法,先假设金盒上的是真话,可依据题意推出矛盾,则证明金盒上的是假话,从而推出结论.

    若金盒上的是真话,则肖像在金盒中,

    那么银盒上的也是真话,这与只有一句真话矛盾,

    故金盒上的是假话,即肖像不在金盒中,

    那么铝盒上的就是真话,银盒上的是假话,

    因此,肖像在银盒中,

    故答案为:银盒.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车，等可能随机顺序前往酒店接嘉宾．某嘉宾突发奇想，设计两种乘车方案．方案一：不乘坐第一辆车，若第二辆车的车序号大于第一辆车的车序号，就乘坐此车，否则乘坐第三辆车；方案二：直接乘坐第一辆车．记方案一与方案二坐到“3号”车的概率分别为P1，P2，则（ ）

    A. P1P2＝ B. P1＝P2＝ C. P1+P2＝ D. P1＜P2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，线段、都是圆的弦，且与垂直且相交于坐标原点，如图所示，设△的面积为，设△的面积为.

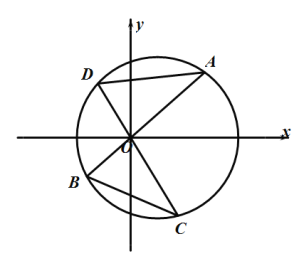
    （1）设点的横坐标为，用表示；

    （2）求证：为定值；

    （3）用、、、表示出，试研究是否有最小值，如果有，求出最小值，并写出此时直线的方程；若没有最小值，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱锥的棱长均为6，其内有个小球，球与三棱锥的四个面都相切，球与三棱锥的三个面和球都相切，如此类推，…，球与三棱锥的三个面和球都相切（，且），则球的体积等于__________，球的表面积等于__________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正方体，过对角线作平面交棱于点E，交棱于点F，则：

    ①四边形一定是平行四边形；

    ②四边形有可能为正方形；

    ③四边形在底面内的投影一定是正方形；

    ④平面有可能垂直于平面.

    其中所有正确结论的序号为（ ）

    A.①②B.②③④C.①④D.①③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平行六面体ABCD－A1B1C1D1中，AA1⊥平面ABCD，且AB＝AD＝2，AA1＝，∠BAD＝120°.

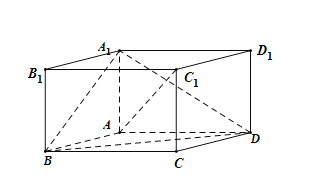
    (1)求异面直线A1B与AC1所成角的余弦值；

    (2)求二面角B－A1D－A的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在棱长为3的正方体ABCDA1B1C1D1中，A1E＝CF＝1.

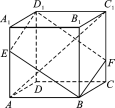
    （1）求异面直线AC1与D1E所成角的余弦值；

    （2）求直线AC1与平面BED1F所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足

    （1）当时，写出所有可能的值；

    （2）当时，若且对任意恒成立，求数列的通项公式；

    （3）记数列的前项和为，若分别构成等差数列，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一青蛙从点开始依次水平向右和竖直向上跳动，其落点坐标依次是，（如图所示，坐标以已知条件为准），表示青蛙从点到点所经过的路程.

    （1）若点为抛物线（）准线上一点，点均在该抛物线上，并且直线经过该抛物线的焦点，证明.

    （2）若点要么落在所表示的曲线上，要么落在所表示的曲线上，并且,试写出（不需证明）；

    （3）若点要么落在所表示的曲线上，要么落在所表示的曲线上，并且，求的表达式.

    查看答案和解析>>

    同步练习册答案