
【题目】已知正方体ABCD﹣A1B1C1D1 , O是底ABCD对角线的交点.求证: 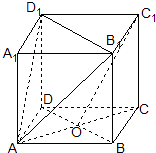
(1)C1O∥面AB1D1;
(2)面BDC1∥面AB1D1 .
【答案】
(1)证明:连接A1C1,设A1C1∩B1D1=O1
连接AO1,∵ABCD﹣A1B1C1D1是正方体
∴A1ACC1是平行四边形
∴A1C1∥AC且A1C1=AC
又O1,O分别是A1C1,AC的中点,
∴O1C1∥AO且O1C1=AO
∴AOC1O1是平行四边形
∴C1O∥AO1,AO1面AB1D1,C1O面AB1D1
∴C1O∥面AB1D1
(2)证明: ![]() 是平行四边形,
是平行四边形,
∴ 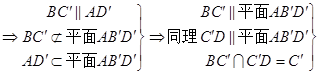 平面C′DB∥平面AB′D′
平面C′DB∥平面AB′D′
【解析】(1)由题意连接A1C1 , 先证明A1ACC1是平行四边形得A1C1∥AC且A1C1=AC,再证AOC1O1是平行四边形,然后利用直线与平面平行的判定定理进行证明;(2)因为AB∥CD∥D′C′,加上AB=CD=D′C′,可证ABC′D′是平行四边形,同理可证C′D∥平面AB′D′,从而求证.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和平面与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行.


科目:高中数学 来源: 题型:
【题目】函数 ![]() 是偶函数,求解下列问题.
是偶函数,求解下列问题.
(1)求θ;
(2)将函数y=f(x)的图象先纵坐标不变,横坐标缩短为原来的 ![]() 倍,再向左平移
倍,再向左平移 ![]() 个单位,然后向上平移1个单位得到y=g(x)的图象,若关于x的方程
个单位,然后向上平移1个单位得到y=g(x)的图象,若关于x的方程 ![]() 在
在 ![]() 有且只有两个不同的根,求m的范围.
有且只有两个不同的根,求m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有 . (写出所有正确说法的序号) ①已知关于x的不等式mx2+mx+2>0的角集为R,则实数m的取值范围是0<m<4.
②已知等比数列{an}的前n项和为Sn , 则Sn、S2n﹣Sn、S3n﹣S2n也构成等比数列.
③已知函数 ![]() (其中a>0且a≠1)在R上单调递减,且关于x的方程
(其中a>0且a≠1)在R上单调递减,且关于x的方程 ![]() 恰有两个不相等的实数解,则
恰有两个不相等的实数解,则 ![]() .
.
④已知a>0,b>﹣1,且a+b=1,则 ![]() +
+ ![]() 的最小值为
的最小值为 ![]() .
.
⑤在平面直角坐标系中,O为坐标原点,| ![]() |=|
|=| ![]() |=|
|=| ![]() |=1,
|=1, ![]() +
+ ![]() +
+ ![]() =
= ![]() ,A(1,1),则
,A(1,1),则 ![]() 的取值范围是
的取值范围是 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合M={x|﹣2≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示以M为定义域,N为值域的函数关系的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且 ![]() .
. 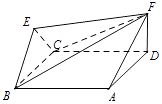
(1)若∠BCD=60°,求证:BC⊥EF;
(2)若∠CBA=60°,求直线AF与平面FBE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cosx,C2:y=sin(2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥![]() 为鳖臑,
为鳖臑, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,三棱锥
,三棱锥![]() 的四个顶点都在球
的四个顶点都在球![]() 的球面上,则球
的球面上,则球![]() 的表面积为( ).
的表面积为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com