
【题目】下列四个函数中,以π为最小正周期,且在区间 ![]() 上为减函数的是( )
上为减函数的是( )
A.y=2|sinx|
B.y=cosx
C.y=sin2x
D.y=|cosx|
科目:高中数学 来源: 题型:
【题目】设F1 , F2分别是C: ![]() +
+ ![]() =1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
=1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为 ![]() ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
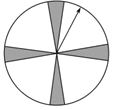
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.
乙商场:从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.问:购买该商品的顾客在哪家商场中奖的可能性大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 年初的时候,国家政府工作报告明确提出,
年初的时候,国家政府工作报告明确提出, ![]() 年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少,
年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少, ![]() 月至
月至![]() 月的用煤量如下表所示:
月的用煤量如下表所示:
月份 |
|
|
|
|
|
|
用煤量 |
|
|
|
|
|
|
(1)由于某些原因, ![]() 中一个数据丢失,但根据
中一个数据丢失,但根据![]() 至
至![]() 月份的数据得出
月份的数据得出![]() 样本平均值是
样本平均值是![]() ,求出丢失的数据;
,求出丢失的数据;
(2)请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)现在用(2)中得到的线性回归方程中得到的估计数据与![]() 月
月![]() 月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过
月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过![]() ,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
(参考公式:线性回归方程![]() ,其中
,其中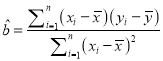
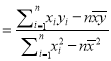 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,a2=2,以后各项由an=an﹣1+an﹣2(n≥3)给出.
(1)写出此数列的前5项;
(2)通过公式bn= ![]() 构造一个新的数列{bn},写出数列{bn}的前4项.
构造一个新的数列{bn},写出数列{bn}的前4项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】联合国教科文组织规定,每年的4月23日是“世界读书日”.某校研究生学习小组为了解本校学生的阅读情况,随机调查了本校400名学生在这一天的阅读时间![]() (单位:分钟),将时间数据分成5组:
(单位:分钟),将时间数据分成5组:![]() ,并整理得到如下频率分布直方图.
,并整理得到如下频率分布直方图.
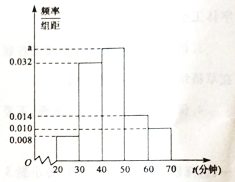
(1)求![]() 的值;
的值;
(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这400名学生中抽取50人参加交流会,则在阅读时间为![]() 的两组中分别抽取多少人?
的两组中分别抽取多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com