
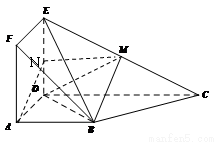
如图,正方形 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直, ,
,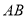 ∥
∥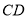 ,
, ,
,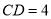 ,
, 为
为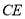 的中点.
的中点.
(1)求证: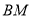 ∥平面
∥平面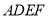 ;
;
(2)求证:平面 平面
平面 ;
;
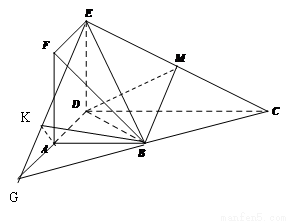
(3)求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.

(1)证明过程详见解析;(2)证明过程详见解析;(3)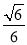 .
.
【解析】
试题分析:本题主要考查中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、二面角等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,作出辅助线MN,N为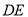 中点,在
中点,在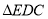 中,利用中位线得到
中,利用中位线得到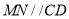 ,且
,且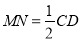 ,结合已知条件,可证出四边形ABMN为平行四边形,所以
,结合已知条件,可证出四边形ABMN为平行四边形,所以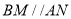 ,利用线面平行的判定,得
,利用线面平行的判定,得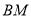 ∥平面
∥平面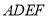 ;第二问,利用面面垂直的性质,判断
;第二问,利用面面垂直的性质,判断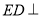 面
面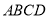 ,再利用已知的边长,可证出
,再利用已知的边长,可证出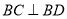 ,则利用线面垂直的判定得
,则利用线面垂直的判定得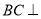 平面BDE,再利用面面垂直的判定得平面
平面BDE,再利用面面垂直的判定得平面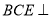 平面
平面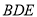 ;第三问,可以利用传统几何法证明二面角的平面角,也可以利用向量法建立空间直角坐标系,求出平面BEC和平面ADEF的法向量,利用夹角公式计算即可.
;第三问,可以利用传统几何法证明二面角的平面角,也可以利用向量法建立空间直角坐标系,求出平面BEC和平面ADEF的法向量,利用夹角公式计算即可.
(1)证明:取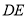 中点
中点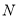 ,连结
,连结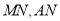 .
.
在△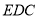 中,
中,
 分别为
分别为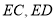 的中点,所以
的中点,所以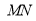 ∥
∥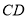 ,且
,且
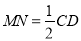 .由已知
.由已知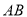 ∥
∥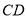 ,
,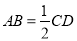 ,所以
,所以
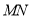 ∥
∥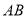 ,且
,且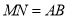 .所以四边形
.所以四边形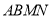 为平行四边形,
为平行四边形,
所以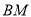 ∥
∥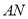 .
.
又因为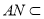 平面
平面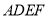 ,且
,且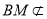 平面
平面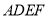 ,
,
所以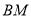 ∥平面
∥平面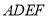 . 4分
. 4分
(2)证明:在正方形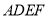 中,
中,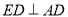 .又因为
.又因为
平面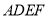
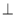 平面
平面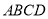 ,且平面
,且平面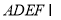 平面
平面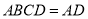 ,
,
所以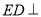 平面
平面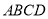 .所以
.所以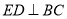 . 6分
. 6分
在直角梯形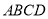 中,
中,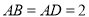 ,
,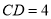 ,可得
,可得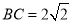 .
.
在△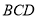 中,
中,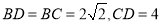 ,所以
,所以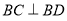 . 7分
. 7分
所以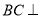 平面
平面 . 8分
. 8分
又因为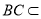 平面
平面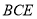 ,所以平面
,所以平面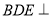 平面
平面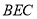 . 9分
. 9分
(3)(方法一)延长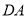 和
和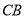 交于
交于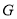 .
.
在平面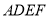 内过
内过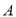 作
作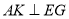 于
于 ,连结
,连结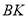 .由平面
.由平面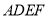
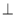 平面
平面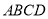 ,
,
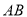 ∥
∥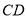 ,
,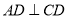 ,平面
,平面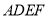
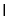 平面
平面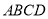 =
=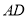 ,
,
得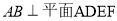 ,于是
,于是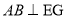 .
.
又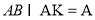 ,
,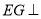 平面
平面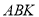 ,所以
,所以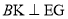 ,
,
于是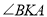 就是平面
就是平面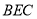 与平面
与平面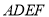 所成锐二面角的
所成锐二面角的
平面角. 12分
由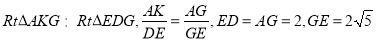 ,得
,得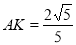 .
.
又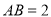 ,于是有
,于是有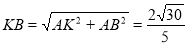 .
.
在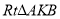 中,
中, .
.
所以平面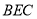 与平面
与平面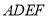 所成锐二面角的余弦值为
所成锐二面角的余弦值为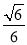 . 14分
. 14分
(方法二)由(2)知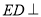 平面
平面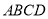 ,且
,且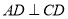 .
.
以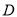 为原点,
为原点,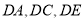 所在直线分别为
所在直线分别为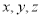 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
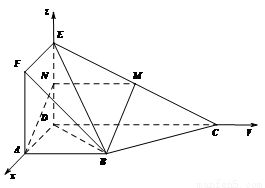
易得 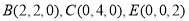 .平面
.平面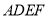 的一个法向量为
的一个法向量为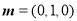 .设
.设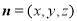 为平面
为平面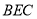 的一个法向量,因为
的一个法向量,因为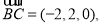 ,
,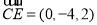 所以
所以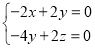 ,令
,令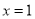 ,得
,得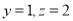 .
.
所以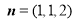 为平面
为平面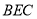 的一个法向量. 12分
的一个法向量. 12分
设平面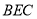 与平面
与平面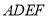 所成锐二面角为
所成锐二面角为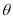 .
.
则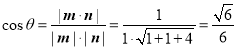 .所以平面
.所以平面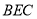 与平面
与平面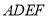 所成锐二面角的余弦值为
所成锐二面角的余弦值为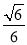 . 14分
. 14分
考点:中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、二面角.


科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:解答题
已知非空有限实数集S的所有非空子集依次记为S1,S2,S3, ,集合Sk中所有元素的平均
值记为bk.将所有bk组成数组T:b1,b2,b3, ,数组T中所有数的平均值记为m(T).
(1)若S={1,2},求m(T);
(2)若S={a1,a2, ,an}(n∈N*,n≥2),求m(T).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:填空题
将函数f(x)=sin(3x+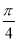 )的图象向右平移
)的图象向右平移 个单位长度,得到函数y=g(x)的图象,则函数y=g(x)在[
个单位长度,得到函数y=g(x)的图象,则函数y=g(x)在[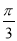 ,
,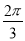 ]上的最小值为 .
]上的最小值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)理科数学试卷(解析版) 题型:选择题
给出下列四个命题,其中假命题是( )
A.从匀速传递的新产品生产流水线上,质检员每10分钟从中抽取一件新产品进行某项指标检测,这样的抽样是分层抽样;
B.样本方差反映了样本数据与样本平均值的偏离程度;
C.在回归分析模型中,残差平方和越小,说明模型的拟合效果越好;
D.设随机变量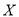 服从正态分布
服从正态分布 ,若
,若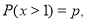 则
则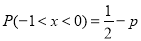 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com