
【题目】已知![]() 的图像可由
的图像可由![]() 的图像平移得到,对于任意的实数
的图像平移得到,对于任意的实数![]() ,均有
,均有![]() 成立,且存在实数
成立,且存在实数![]() ,使得
,使得![]() 为奇函数.
为奇函数.
(Ⅰ)求函数![]() 的解析式.
的解析式.
(Ⅱ)函数![]() 的图像与直线
的图像与直线![]() 有两个不同的交点
有两个不同的交点![]() ,
, ![]() ,若
,若![]() ,
,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】一个几何体,它的下面是一个圆柱,上面是一个圆锥,并且圆锥的底面与圆柱的上底面重合,圆柱的底面直径为3 cm,高为4 cm,圆锥的高为3 cm,画出此几何体的直观图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是临江公园内一个等腰三角形形状的小湖(假设湖岸是笔直的),其中两腰
是临江公园内一个等腰三角形形状的小湖(假设湖岸是笔直的),其中两腰![]() 米,
米,![]() .为了给市民营造良好的休闲环境,公园管理处决定在湖岸
.为了给市民营造良好的休闲环境,公园管理处决定在湖岸![]() ,
,![]() 上分别取点
上分别取点![]() ,
,![]() (异于线段端点),在湖上修建一条笔直的水上观光通道
(异于线段端点),在湖上修建一条笔直的水上观光通道![]() (宽度不计),使得三角形
(宽度不计),使得三角形![]() 和四边形
和四边形![]() 的周长相等.
的周长相等.

(1)若水上观光通道的端点![]() 为线段
为线段![]() 的三等分点(靠近点
的三等分点(靠近点![]() ),求此时水上观光通道
),求此时水上观光通道![]() 的长度;
的长度;
(2)当![]() 为多长时,观光通道
为多长时,观光通道![]() 的长度最短?并求出其最短长度.
的长度最短?并求出其最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。
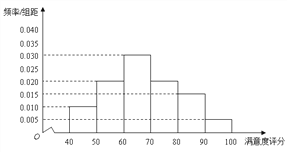
A地区用户满意度评分的频率分布直方图

B地区用户满意度评分的频数分布表
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的满意度等级为不满意的概率大?说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABCDEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.

(1)求证:BF⊥平面ACFD;
(2)求二面角B-AD-F的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过P(4,-2),Q(-1,3)两点,且圆心在x轴上。
(1)求直线PQ的方程;
(2)圆C的方程;
(3)若直线l∥PQ,且l与圆C交于点A,B,且以线段AB为直径的圆经过坐标原点,求直线l的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() ,侧面
,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(1)求证: ![]() 平面
平面![]() ;
;
(2)如果三棱锥![]() 的体积为
的体积为![]() ,求点
,求点![]() 到面
到面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)在平行四边形![]() 中,得出
中,得出![]() ,进而得到
,进而得到![]() ,证得
,证得![]() 底面
底面![]() ,得出
,得出![]() ,进而证得
,进而证得![]() 平面
平面![]() .
.
(2)由![]() 到面
到面![]() 的距离为
的距离为![]() ,所以
,所以![]() 面
面![]() ,
, ![]() 为
为![]() 中点,即可求解
中点,即可求解![]() 的值.
的值.
试题解析:
证明:(1)在平行四边形![]() 中,因为
中,因为![]() ,
, ![]() ,
,
所以![]() ,由
,由![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,得
的中点,得![]() ,所以
,所以![]() .
.
侧面![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 底面
底面![]() .
.
又因为![]() 底面
底面![]() ,所以
,所以![]() .
.
又因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
解:(2)![]() 到面
到面![]() 的距离为1,所以
的距离为1,所以![]() 面
面![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的极值;
的极值;
(3)若函数![]() 在区间
在区间![]() 上是增函数,试确定
上是增函数,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com