
(12分)设函数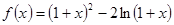 .(1)求
.(1)求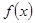 的单调区间;(2)当
的单调区间;(2)当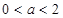 时,求函数
时,求函数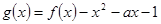 在区间
在区间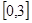 上的最小值.
上的最小值.
(1)函数的单调递增区间为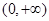 ,单调递减区间为
,单调递减区间为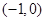 .
.
(2)当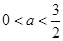 时,
时,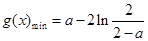 ;当
;当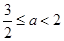 时,
时,
【解析】本试题考查了函数的单调性和函数的最值的求解的综合运用。
(1)先求解函数的定义域和导函数,然后解二次不等式得到单调区间。
(2)构造函数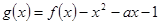 利用导数判定单调性,进而得到在给定区间上
利用导数判定单调性,进而得到在给定区间上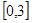 结论。
结论。
解:(1)定义域为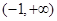 ,
,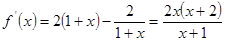
令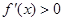 ,则
,则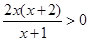 ,所以
,所以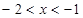 或
或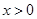 因为定义域为
因为定义域为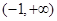 ,所以
,所以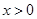 .
.
令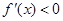 ,则
,则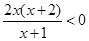 ,所以
,所以 .因为定义域为
.因为定义域为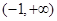 ,所以
,所以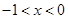 .
.
所以函数的单调递增区间为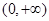 ,单调递减区间为
,单调递减区间为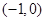 .
.
(2)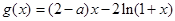 (
(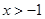 ),
),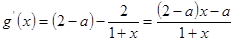 .
.
因为0<a<2,所以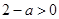 ,
,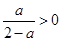 .令
.令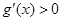 可得
可得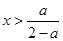 .所以函数
.所以函数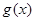 在
在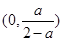 上为减函数,在
上为减函数,在 上为增函数.①当
上为增函数.①当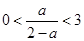 ,即
,即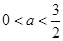 时,在区间
时,在区间 上,
上,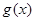 在
在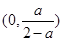 上为减函数,在
上为减函数,在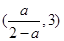 上为增函数.所以
上为增函数.所以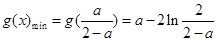 .②当
.②当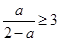 ,即
,即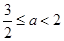 时,
时,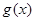 在区间
在区间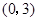 上为减函数.所以
上为减函数.所以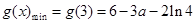 .综上所述,当
.综上所述,当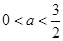 时,
时,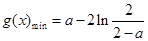 ;当
;当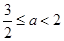 时,
时,


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)
设函数,,是的一个极大值点.
(Ⅰ)若,求的取值范围;
(Ⅱ) 当是给定的实常数,设是的3个极值点,问是否存在实数,可找到,使得的某种排列(其中=)依次成等差数列?若存在,求所有的及相应的;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011届云南省蒙自高中高三1月月考数学理卷 题型:解答题
((本小题满分12分)
设函数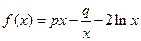 ,且
,且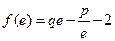 ,其中
,其中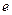 是自然对数的底数.
是自然对数的底数.
(I)求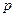 与
与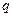 的关系;
的关系;
(II)若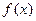 在其定义域内为单调函数,求
在其定义域内为单调函数,求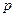 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2010-2011学年海南省高三上学期第二次月考理科数学卷 题型:解答题
(本题满分12分)
设函数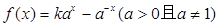 是定义域为R上的奇函数.
是定义域为R上的奇函数.
(1)若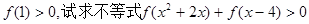 的解集;
的解集;
(2)若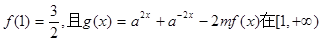 上的最小值为
上的最小值为 ,
,
求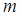 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(陕西) 题型:解答题
(本小题满分12分)
设函数f(x)=a-b,其中向量a=(m,cos2x),b=(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点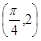 ,
,
(Ⅰ)求实数m的值;
(Ⅱ)求函数f(x)的最小值及此时x的值的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com