
【题目】如图,四棱锥![]() 的底面为直角梯形,
的底面为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(Ⅰ)求证:![]() 平面
平面![]()
(Ⅱ)若平面![]() 平面
平面![]() ,异面直线
,异面直线![]() 与
与![]() 所成角为60°,且
所成角为60°,且![]() 是钝角三角形,求二面角
是钝角三角形,求二面角![]() 的正弦值
的正弦值
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明四边形
,证明四边形![]() 为平行四边形,得到
为平行四边形,得到![]() 即可
即可
(Ⅱ)由条件得出![]() ,然后证明
,然后证明![]() 平面
平面![]() ,然后以
,然后以![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴建立空间直角坐标系,分别求出平面
轴建立空间直角坐标系,分别求出平面![]() 和平面
和平面![]() 的法向量即可.
的法向量即可.
(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为![]() 为
为![]() 的中点,则
的中点,则![]() ,且
,且![]() ,
,
又![]() ,且
,且![]() ,所以
,所以![]() ,
,![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
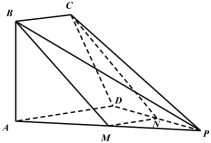
(Ⅱ)由题意可知![]() ,所以
,所以![]() 或其补角为异面直线
或其补角为异面直线![]() 与
与![]() 所成角,
所成角,
又![]() ,
,![]() 为钝角三角形,所以
为钝角三角形,所以![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
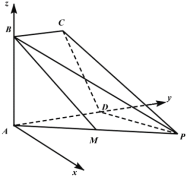
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
向量![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]()
由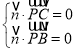 得
得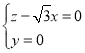 ,令
,令![]() ,
,
得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
同理可得平面![]() 的一个法向量为
的一个法向量为![]()
设二面角![]() 的平面角为
的平面角为![]() ,
,
则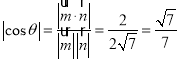
则![]()
故二面角![]() 的正弦值为
的正弦值为![]()


科目:高中数学 来源: 题型:
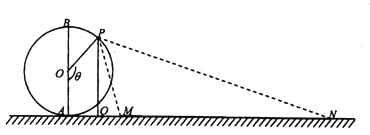
【题目】如图,摩天轮的半径![]() 为
为![]() ,它的最低点
,它的最低点![]() 距地面的高度忽略不计.地上有一长度为
距地面的高度忽略不计.地上有一长度为![]() 的景观带
的景观带![]() ,它与摩天轮在同一竖直平面内,且
,它与摩天轮在同一竖直平面内,且![]() .点
.点![]() 从最低点
从最低点![]() 处逆时针方向转动到最高点
处逆时针方向转动到最高点![]() 处,记
处,记![]() .
.
(1)当![]() 时,求点
时,求点![]() 距地面的高度
距地面的高度![]() ;
;
(2)试确定![]() 的值,使得
的值,使得![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东京夏季奥运会推迟至2021年7月23日至8月8日举行,此次奥运会将设置4![]() 100米男女混泳接力赛这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳
100米男女混泳接力赛这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳![]() 蛙泳
蛙泳![]() 蝶泳
蝶泳![]() 自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场.若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者蛙泳,剩下2名运动员四种泳姿都可以承担,则中国队参赛的安排共有( )
自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场.若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者蛙泳,剩下2名运动员四种泳姿都可以承担,则中国队参赛的安排共有( )
A.144种B.8种C.24种D.12种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设X是有限集,t为正整数,F是包含t个子集的子集族:F=![]() .如果F中的部分子集构成的集族S满足:对S中任意两个不相等的集合A、B,
.如果F中的部分子集构成的集族S满足:对S中任意两个不相等的集合A、B,![]() 均不成立,则称S为反链.设S1为包含集合最多的反链,S2是任意反链.证明:存在S2到S1的单射f,满足
均不成立,则称S为反链.设S1为包含集合最多的反链,S2是任意反链.证明:存在S2到S1的单射f,满足![]() 或
或![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
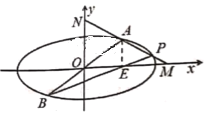
【题目】如图,已知椭圆C:![]() 过原点的直线与椭圆交于A,B两点(点A在第一象限),过点A作x轴的垂线,垂足为点
过原点的直线与椭圆交于A,B两点(点A在第一象限),过点A作x轴的垂线,垂足为点![]() ,设直线BE与椭圆的另一交点为P,连接AP得到直线l,交x轴于点M,交y轴于点N.
,设直线BE与椭圆的另一交点为P,连接AP得到直线l,交x轴于点M,交y轴于点N.
(1)若![]() ,求直线AP的斜率;
,求直线AP的斜率;
(2)记![]() 的面积分别为S1,S2,S3,求
的面积分别为S1,S2,S3,求![]() 的的最大值.
的的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com