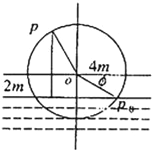
【题目】如图，一个水轮的半径为4m，水轮圆心O距离水面2m，已知水轮每分钟转动5圈，如果当水轮上点P从水中浮现时（图中点p0）开始计算时间．
（1）将点p距离水面的高度z（m）表示为时间t（s）的函数；
（2）点p第一次到达最高点大约需要多少时间？
【答案】（1）
（2）点P第一次到达最高点大约需要4s．
【解析】试题分析：（1）令函数为
，由题意可知函数最大值与最小值，由两最值可得振幅
与
，再由每分钟转过的角度可得周期，利用周期与
的关系可得其值，再将起始位置时， 
满足函数表达式代入可得
值；（2）当函数取最值时，求出对应的
值，取最小正值，即为所需要时间．
试题解析：（1）依题意可知z的最大值为6，最小为﹣2，
∴
；
∵op每秒钟内所转过的角为
，得z=4sin
，
当t=0时，z=0，得sinφ=﹣
，即φ=﹣
，故所求的函数关系式为
z=4sin
+2
（2）令z=4sin
+2=6，得sin=1，
取
，得t=4，
故点P第一次到达最高点大约需要4s．
科目：高中数学 来源： 题型：
【题目】一盒中装有12个球，其中5个红球，4个黑球，2个白球，1个绿球．从中随机取出1球，求：
(1)取出1球是红球或黑球的概率；
(2)取出1球是红球或黑球或白球的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知中国某手机品牌公司生产某款手机的年固定成本为40万元，每生产1万部还需另投入16万元．设公司一年内共生产该款手机
万部并全部销量完，每万部的销售收入为
万元，且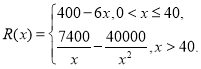
（1）写出年利润
万元关于年产量
（万部）的函数解析式；
（2）当年产量为多少万部时，公司在该款手机的生产中所获得的利润最大？并求出最大利润．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表：
(1) 算出线性回归方程
; (a,b精确到十分位)
(2)气象部门预测下个月的平均气温约为3℃,据此估计,求该商场下个月毛衣的销售量.
(参考公式：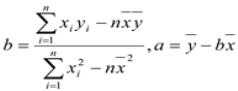
)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f(x)＝
(m＞0，n＞0)．
(1) 当m＝n＝1时，求证：f(x)不是奇函数；
(2) 设f(x)是奇函数，求m与n的值；
(3) 在(2)的条件下，求不等式f(f(x))＋f
<0的解集．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数据x1，x2，x3，…，xn是普通职工n（n≥3，n∈N*）个人的年收入，设这n个数据的中位数为x，平均数为y，方差为z，如果再加上世界首富的年收入xn+1，则这n+1个数据中，下列说法正确的是
A. 年收入平均数大大增大，中位数一定变大，方差可能不变
B. 年收入平均数大大增大，中位数可能不变，方差变大
C. 年收入平均数大大增大，中位数可能不变，方差也不变
D. 年收入平均数可能不变，中位数可能不变，方差可能不变
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=（
）x.
（Ⅰ）当x∈[﹣1，1]时，求函数y=[f（x）]2﹣2af（x）+3的最小值g（a）；
（Ⅱ）在（Ⅰ）的条件下，是否存在实数m＞n＞3，使得g（x）的定义域为[n，m]，值域为[n2，m2]？若存在，求出m、n的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等边三角形，已知AD=4， 
，AB=2CD=8．
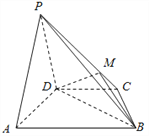
（1）设M是PC上的一点，证明：平面MBD⊥平面PAD；
（2）当M点位于线段PC什么位置时，PA∥平面MBD？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
