
(1)甲不站在两端;
(2)甲、乙二人不能站在两端;
(3)甲、乙二人之间间隔两个人;
(4)四名男生站在一起,三名女生站在一起;
(5)男女互相间隔开;
(6)三名女生排列顺序一定.
解析:(1)方法一:因为甲不在两端,分两步排队,首先从甲以外的6个人中任选两人站在左、右两端,有![]() 种方法,然后让剩下的5个人(其中包括甲)站在中间的5个位置上,有
种方法,然后让剩下的5个人(其中包括甲)站在中间的5个位置上,有![]() 种方法,因此共有
种方法,因此共有![]() ·
·![]() =3 600种站法.
=3 600种站法.
(注:这里使用的方法称为“位置分析法”)
方法二:因为甲不在两端,分两步排队,首先排甲,有![]() 种方法,第二步让其他6人站在其他6个位置上,有
种方法,第二步让其他6人站在其他6个位置上,有![]() 种方法,故有
种方法,故有![]() ·
·![]() =3 600种站法.
=3 600种站法.
(注:这里使用的方法称为“元素分析法”)
方法三:第一步先让甲以外的人站队,有![]() 种方法,第二步让甲插入这6个人之间的空当中,有
种方法,第二步让甲插入这6个人之间的空当中,有![]() 种,故共有
种,故共有![]() ·
·![]() =3 600种站法.
=3 600种站法.
(注:这种解法称为“插空法”)
方法四:在排队时,对7个人,不考虑甲的站法要求任意排列,有![]() 种方法,但其中包括甲在左端或右端的情况有2
种方法,但其中包括甲在左端或右端的情况有2![]() 种方法,因此共有
种方法,因此共有![]() -2
-2![]() =3 600种站法.
=3 600种站法.
(注:这种解法称为“间接法”或“排异法”)
(2)方法一:甲、乙两人为特殊元素,先考虑甲、乙的站法,除两端的其余5个不同位置都可排甲、乙,有![]() 种排法,再考虑其余5个元素的排法有
种排法,再考虑其余5个元素的排法有![]() 种,根据分步计数原理,甲、乙二人不能站在两端的排法有
种,根据分步计数原理,甲、乙二人不能站在两端的排法有![]() ·
·![]() =5×4×5!=2 400种.
=5×4×5!=2 400种.
方法二:甲、乙两人不能站在两端,应包括同时不在两端,某一人在两端,故用排异法,应减去两种情况,同时在两端, 有![]() ·
·![]() 种,某一人在两端,有2·
种,某一人在两端,有2·![]() ·
·![]() ·
·![]() 种,故有
种,故有![]() -
-![]() ·
·![]() -2
-2![]() ·
·![]() ·
·![]() =2 400种不同站法.
=2 400种不同站法.
(3)分三步:第一步,从甲、乙以外的5个人中任选2人排在甲、乙之间的两个位置上,有![]() 种方法,第二步,把甲、乙及中间2人看作一个元素与剩下的3个人作全排列,有
种方法,第二步,把甲、乙及中间2人看作一个元素与剩下的3个人作全排列,有![]() 种方法,第三步,对甲、乙进行全排列,故共有
种方法,第三步,对甲、乙进行全排列,故共有![]() ·
·![]() ·
·![]() =960种不同站法.
=960种不同站法.
(4)方法一:男生站在前4个位置上有![]() 种站法,女生站在后三个位置上有
种站法,女生站在后三个位置上有![]() 种站法,男女生站成一排是分两步完成的,因此这种站法共有
种站法,男女生站成一排是分两步完成的,因此这种站法共有![]() ·
·![]() 种,而女生站在前三个位置上,男生站在后四个位置上也有
种,而女生站在前三个位置上,男生站在后四个位置上也有![]() ·
·![]() 种站法,这两种站法都符合要求,所以四名男生站在一起、三名女生也站在一起的站法共有2
种站法,这两种站法都符合要求,所以四名男生站在一起、三名女生也站在一起的站法共有2![]() ·
·![]() =288种.
=288种.
方法二:把站在一起的四名男生看作一个整体,站在一起的女生也看成一个整体,这样解决这个问题可分为三个步骤:选排男生、女生这两个整体,有![]() 种排法,然后排四名男生,有
种排法,然后排四名男生,有![]() 种排法,最后排三名女生,有
种排法,最后排三名女生,有![]() 种排法,根据分步计数原理,将四名男生站在一起,三名女生站在一起的站法有
种排法,根据分步计数原理,将四名男生站在一起,三名女生站在一起的站法有![]() ·
·![]() ·
·![]() =288种.
=288种.
(注:此种方法称为“捆绑法”)
(5)不妨先排男生,有![]() 种排法,在四名男生间的三个间隔共有三个位置安排三名女生,有
种排法,在四名男生间的三个间隔共有三个位置安排三名女生,有![]() 种,因此共有
种,因此共有![]() ·
·![]() 种排法符合要求,故四名男生三名女生相间排列的排法共有
种排法符合要求,故四名男生三名女生相间排列的排法共有![]() ·
·![]() =144种.
=144种.
(6)在7个位置上任意排列7名学生,有排法![]() 种,由于女生的顺序一定,而在
种,由于女生的顺序一定,而在![]() 中每一种情况均以
中每一种情况均以![]() 计算,故三名女生顺序一定的排法有
计算,故三名女生顺序一定的排法有![]() =840种.
=840种.
小结:“元素分析法”“位置分析法”是解决排列问题的基本方法,它们的共同点是先考虑特殊元素的要求,以特殊元素为轴心展开讨论;解决带有限制条件的排列问题除“轴心法”外,还有间接法即淘汰法.直接法、间接法、插入法、捆绑法,都是分析问题的常用方法.


科目:高中数学 来源: 题型:
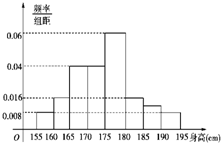 从某校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图.
从某校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图.| 组 别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 |
| 样本数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com