
【题目】如图,在棱长为2的正方体![]() 中,
中,![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在平面
在平面![]() 内,若直线
内,若直线![]() 与平面
与平面![]() 没有公共点,则线段
没有公共点,则线段![]() 长的最小值是( )
长的最小值是( )
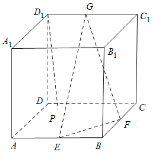
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
方法一:连接![]() ,可证得平面
,可证得平面![]() 平面
平面![]() ,根据题意得到点
,根据题意得到点![]() 在直线
在直线![]() 上,再根据图形的特点得当
上,再根据图形的特点得当![]() 为
为![]() 中点时,线段
中点时,线段![]() 的长度最小,于是可得所求.
的长度最小,于是可得所求.
方法二:连接![]() ,可得直线
,可得直线![]() 平面
平面![]() .延长
.延长![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,则
,则![]() ,所以点
,所以点![]() 在直线
在直线![]() 上,结合图形得当
上,结合图形得当![]() 为
为![]() 中点时,线段
中点时,线段![]() 的长度最小,进而可得答案.
的长度最小,进而可得答案.
解法一:如图,连接![]() ,
,
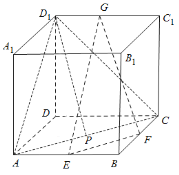
由![]() 分别为
分别为![]() 的中点可得
的中点可得![]() ,
,
所以![]() 平面
平面![]() .
.
同理可得![]() 平面
平面![]() ,
,
所以可得平面![]() 平面
平面![]() .
.
因为![]() 与平面
与平面![]() 没有公共点,
没有公共点,
所以直线![]() 平面
平面![]() ,
,
所以点![]() 在直线
在直线![]() 上,
上,
所以当![]() 为
为![]() 中点时,线段
中点时,线段![]() 的长度最小,此时
的长度最小,此时![]() .
.
故选D.
解法二:如图,连接![]() ,
,

因为直线![]() 与平面
与平面![]() 没有公共点,
没有公共点,
所以直线![]() 平面
平面![]() .
.
延长![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,
,
则![]() ,
,
所以点![]() 在直线
在直线![]() 上,
上,
易得当![]() 为
为![]() 中点时,线段
中点时,线段![]() 的长度最小,此时
的长度最小,此时![]() .
.
故选D.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】某工厂拟制造一个如图所示的容积为36π立方米的有盖圆锥形容器.
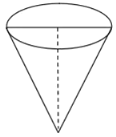
(1)若该容器的底面半径为6米,求该容器的表面积;
(2)当容器的高为多少米时,制造该容器的侧面用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() ,若曲线
,若曲线![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)求点![]() 到
到![]() 、
、![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·吉林期末]一个袋中装有6个大小形状完全相同的球,球的编号分别为1,2,3,4,5,6.
(1)从袋中随机抽取两个球,求取出的球的编号之和为6的概率;
(2)先后有放回地随机抽取两个球,两次取的球的编号分别记为![]() 和
和![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 作垂直于
作垂直于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() ,
,![]() 两点,且以线段
两点,且以线段![]() 为直径的圆过点
为直径的圆过点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为曲线
为曲线![]() :
:![]() 上的动点,求
上的动点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在抽取彩票“双色球”中奖号码时,有33个红色球,每个球的编号分别为01,02,…,33.一位彩民用随机数表法选取6个号码作为6个红色球的编号,选取方法是从下面的随机数表中第1行第6列的数字3开始,从左向右读数,则依次选出的第3个红色球的编号为( )
49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 |
57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
A.21B.32C.09D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,椭圆
,椭圆![]() 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且线段
,且线段![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年入冬以来,我市天气反复.在下图中统计了我市上个月前15天的气温,以及相对去年同期的气温差(今年气温-去年气温,单位:摄氏度),以下判断错误的是( )
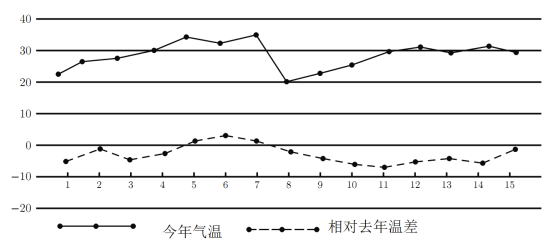
A.今年每天气温都比去年气温低B.今年的气温的平均值比去年低
C.今年8-12号气温持续上升D.今年8号气温最低
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com