
已知向量a=3e1-2e2,b=4e1+e2,其中e1=(1,0),e2=(0,1),求:
(1)a·b,|a+b|;(2)a与b的夹角的余弦值.
(1)10,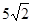 ;(2)
;(2)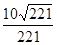 .
.
解析试题分析:先根据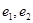 向量是互相垂直的单位向量表示出向量要用的两个向量,然后根据向量的数量积运算和向量模的运算求出答案.(2)先求出向量的模长,然后根据cosθ的表示式将数值代入即可得到答案.本题主要考查向量的模、平面向量的坐标运算、数量积运算,本题解题的关键是根据所给的两个单位向量,写出要用的向量的坐标.
向量是互相垂直的单位向量表示出向量要用的两个向量,然后根据向量的数量积运算和向量模的运算求出答案.(2)先求出向量的模长,然后根据cosθ的表示式将数值代入即可得到答案.本题主要考查向量的模、平面向量的坐标运算、数量积运算,本题解题的关键是根据所给的两个单位向量,写出要用的向量的坐标.
(1)a=3(1,0)-2(0,1)=(3,-2),b=4(1,0)+(0,1)=(4,1),a·b=3×4+(-2)×1=10,
∵|a+b|2=(a+b)2=a2+2a·b+b2=|a|2+20+|b|2=13+20+17=50,∴|a+b|=5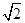
(2)cos〈a,b〉=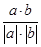 =
=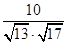 =
=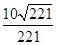 .
.
考点:平面向量数量积的坐标表示、模、夹角.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
已知抛物线 :
: 的焦点为
的焦点为 ,若过点
,若过点 且斜率为
且斜率为 的直线与抛物线相交于
的直线与抛物线相交于 两点,且
两点,且 .
.
(1)求抛物线 的方程;
的方程;
(2)设直线 为抛物线
为抛物线 的切线,且
的切线,且 ∥
∥ ,
, 为
为 上一点,求
上一点,求 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com