
分析 先解出y得y=$\frac{2x+5}{x-2}$(x>2),再裂项xy=2•[(x-2)+$\frac{9}{x-2}$]+13,最后用基本不等式求最值.
解答 解:由$\frac{3}{1+x}$+$\frac{3}{1+y}$=1解得y=$\frac{2x+5}{x-2}$(x>2),
所以,xy=x•$\frac{2x+5}{x-2}$
=$\frac{2x^2+5x}{x-2}$=$\frac{2(x-2)^2+13(x-2)+18}{x-2}$
=2•[(x-2)+$\frac{9}{x-2}$]+13
≥2$\sqrt{(x-2)•\frac{9}{x-2}}$+13=25,
当且仅当:x=5时,取“=”,此时,y=5,
即xy的最小值为:25,
故答案为:25.
点评 本题主要考查了基本不等式在求最值问题中的应用,通过消元,配方,裂项,基本基本不等式求最值,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
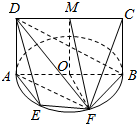 如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.
如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com