
 ,求二面角A-PB-D的余弦值.
,求二面角A-PB-D的余弦值.
 (1)证明:连接OA,则∵AB=AF,BF的中点O,∴AO⊥BF
(1)证明:连接OA,则∵AB=AF,BF的中点O,∴AO⊥BF ,
,
 ,0),B(
,0),B( ,0,0),P(0,0,
,0,0),P(0,0, ),D(0,
),D(0, ,0)
,0) ,
, ,
,
 ,则
,则 ,
, ,领z=-1,可得
,领z=-1,可得




科目:高中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,M是PA的中点.
,M是PA的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
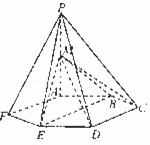
如图所示,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,AB=2,PA=2![]() ,M是PA的中点.
,M是PA的中点.
(1)求证:平面PCD∥平面MBE;
(2)设PA=λAB,当二面角D﹣ME﹣F的大小为135°,求λ的值.
查看答案和解析>>
科目:高中数学 来源:2012年江西省九江市高考数学一模试卷(文科)(解析版) 题型:解答题
 ,M是PA的中点.
,M是PA的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com