
【题目】如图,矩形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM. 
(1)求证:平面D′AM⊥平面ABCM;
(2)若E为D′B的中点,求二面角E﹣AM﹣D′的余弦值.
【答案】
(1)证明:由题知,在矩形ABCD中,∠AMD=∠BMC=45°,
∴∠AMB=90°,
又D'A⊥BM,∴BM⊥面D'AM,
∵BM面ABCM,
∴面ABCM⊥面D'AM
(2)解:由(Ⅰ)知,在平面D'AM内过M作直线NM⊥MA,则NM⊥平面ABCM,
故以M为原点, ![]() 分别为x,y,z轴的正方向建立空间直角坐标系,
分别为x,y,z轴的正方向建立空间直角坐标系,
则M(0,0,0),A(2,0,0),B(0,2,0),D'(1,0,1),
于是 ![]() ,
, ![]() ,
, ![]() ,
,
设平面EAM的法向量为 ![]() ,
,
则  令y=1,得平面EAM的一个法向量
令y=1,得平面EAM的一个法向量 ![]() ,
,
平面D'AM的一个法向量为 ![]() ,
,
故 ![]() ,
,
即二面角E﹣AM﹣D'的余弦值为 ![]() .
.

【解析】(Ⅰ)推导出∠AMB=90°,D'A⊥BM,从而BM⊥面D'AM,由此能证明面ABCM⊥面D'AM.(Ⅱ)在平面D'AM内过M作直线NM⊥MA,以M为原点, ![]() 分别为x,y,z轴的正方向建立空间直角坐标系,利用向量法能求出二面角E﹣AM﹣D'的余弦值.
分别为x,y,z轴的正方向建立空间直角坐标系,利用向量法能求出二面角E﹣AM﹣D'的余弦值.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】近期“共享单车”在全国多个城市持续升温,某移动互联网机构通过对使用者的调查得出,现在市场上常见的八个品牌的“共享单车”的满意度指数如茎叶图所示:
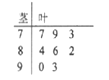
(Ⅰ)求出这组数据的平均数和中位数;
(Ⅱ)某用户从满意度指数超过80的品牌中随机选择两个品牌使用,求所选两个品牌的满意度指数均超过85的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经国务院批复同意,郑州成功入围国家中心城市,某校学生团针对“郑州的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图1所示茎叶图. 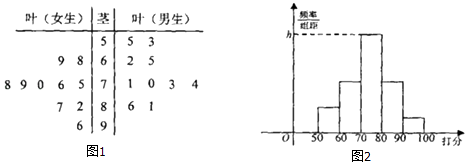
(Ⅰ)分别计算男生女生打分的平均分,并用数学特征评价男女生打分的数据分布情况;
(Ⅱ)如图2按照打分区间[0,60)、[60,70)、[70,80)、[80,90)、[90,100]绘制的直方图中,求最高矩形的高;
(Ⅲ)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+2)x+alnx,其中常数a>0. (Ⅰ)当a>2时,求函数f(x)的单调递增区间;
(Ⅱ)设定义在D上的函数y=h(x)在点P(x0 , h(x0))处的切线方程为l:y=g(x),若 ![]() >0在D内恒成立,则称P为函数y=h(x)的“类对称点”.当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
>0在D内恒成立,则称P为函数y=h(x)的“类对称点”.当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别是F1 , F2 , 过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点分别是F1 , F2 , 过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( ) 
A.小球第10次着地时向下的运动共经过的路程
B.小球第11次着地时向下的运动共经过的路程
C.小球第10次着地时一共经过的路程
D.小球第11次着地时一共经过的路程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2. 
(1)求证:平面ABF⊥平面PQFE;
(2)若PQ与平面ABF所成的角为 ![]() ,求三棱锥P﹣QDE的体积.
,求三棱锥P﹣QDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,PC⊥平面ABCD,点E在棱PA上. 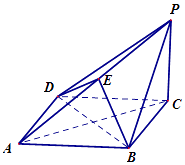
(Ⅰ)求证:直线BD⊥平面PAC;
(Ⅱ)若PC∥平面BDE,求证:AE=EP;
(Ⅲ)是否存在点E,使得四面体A﹣BDE的体积等于四面体P﹣BDC的体积的 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com