
【题目】已知函数f(x)=2cosx(sinx﹣cosx)+m(m∈R),将y=f(x)的图象向左平移 ![]() 个单位后得到y=g(x)的图象,且y=g(x)在区间
个单位后得到y=g(x)的图象,且y=g(x)在区间 ![]() 内的最大值为
内的最大值为 ![]() .
.
(1)求实数m的值;
(2)在△ABC中,内角A、B、C的对边分别是a、b、c,若 ![]() ,且a+c=2,求△ABC的周长l的取值范围.
,且a+c=2,求△ABC的周长l的取值范围.
【答案】
(1)解:由题设得 ![]() ,
,
∴ ![]() ,
,
因为当 ![]() 时,
时, ![]() ,
,
所以由已知得 ![]() ,即
,即 ![]() 时,
时, ![]() ,
,
所以m=1;
(2)解:由已知 ![]() ,
,
因为三角形中 ![]() ,
,
所以 ![]() ,
,
所以 ![]() ,即
,即 ![]() ,
,
又因为a+c=2,由余弦定理得: ![]() ,
,
当且仅当a=c=1时等号成立,
又∵b<a+c=2,∴1≤b<2,
所以△ABC的周长l=a+b+c∈[3,4),
故△ABC的周长l的取值范围是[3,4).
【解析】(1)先利用两角和公式和对函数解析式化简整理,根据图象的平移确定g(x)的解析式,根据x的范围和三角函数的图象与性质确定g(x)的最大值的解析式,求得m.(2)根据第一问中函数的解析式确定B的值,进而利用余弦定理和基本不等式确定b的范围,最后确定周长的范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在某中学举行的环保知识竞赛中,将三个年级参赛的学生的成绩进行整理后分为5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组,已知第二小组的频数是40,则成绩在80~100分的学生人数是( )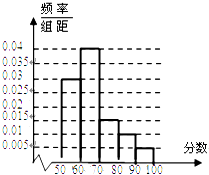
A.15
B.18
C.20
D.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
(Ⅰ)若 ![]() ,求k的值;
,求k的值;
(Ⅱ)求四边形AEBF面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,a,b,c分别为角A,B,C的对边,csinC﹣asinA=( ![]() c﹣b)sinB.
c﹣b)sinB.
(Ⅰ)求角A;
(Ⅱ)若a=1,求三角形ABC面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于下列四个命题
p1:x0∈(0,+∞),( ![]() )x0<(
)x0<( ![]() )x0
)x0
p2:x0∈(0,1), ![]() x0>
x0> ![]() x0
x0
p3:x∈(0,+∞),( ![]() )x>
)x> ![]() x
x
p4:x∈(0, ![]() ),(
),( ![]() )x<
)x< ![]() x.
x.
其中的真命题是( )
A.p1 , p3
B.p1 , p4
C.p2 , p3
D.p2 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 ![]() (t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位.且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=6sinθ.
(t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位.且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=6sinθ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B.若点P的坐标为(1,2),求|PA|+|PB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;
(2)当x>0时, ![]() 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(3)试证明:(1+12)(1+23)(1+34)…(1+n(n+1))>e2n﹣3 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,M是边BC的中点,tan∠BAM= ![]() ,cos∠AMC=﹣
,cos∠AMC=﹣ ![]() (Ⅰ)求角B的大小;
(Ⅰ)求角B的大小;
(Ⅱ)若角∠BAC= ![]() ,BC边上的中线AM的长为
,BC边上的中线AM的长为 ![]() ,求△ABC的面积.
,求△ABC的面积.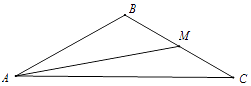
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用 ![]() (单位:元)关于月用电量
(单位:元)关于月用电量 ![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的占80%,求 ![]() 的值;
的值;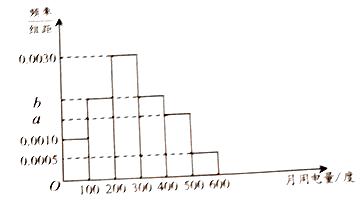
(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com