
【题目】在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)上一点P( ![]() ,m)到准线的距离与到原点O的距离相等,抛物线的焦点为F.
,m)到准线的距离与到原点O的距离相等,抛物线的焦点为F.
(1)求抛物线的方程;
(2)若A为抛物线上一点(异于原点O),点A处的切线交x轴于点B,过A作准线的垂线,垂足为点E.试判断四边形AEBF的形状,并证明你的结论.
【答案】
(1)解:抛物线y2=2px(p>0)的焦点F( ![]() ,0),准线方程为x=﹣
,0),准线方程为x=﹣ ![]() ,
,
由题意点 ![]() 到准线的距离为|PO|,
到准线的距离为|PO|,
由抛物线的定义,可得点P到准线的距离为|PF|,
即有|PO|=|PF|,即点 ![]() 在线段OF的中垂线上,
在线段OF的中垂线上,
则 ![]() =
= ![]() ,解得p=3,则抛物线的方程为y2=6x
,解得p=3,则抛物线的方程为y2=6x
(2)解:四边形AEBF为菱形.
证明:抛物线y2=6x的焦点为F( ![]() ,0),准线方程为x=﹣
,0),准线方程为x=﹣ ![]() ,
,
由抛物线的对称性,设点 ![]() 在x轴的上方,
在x轴的上方,
由y2=6x,两边对x求导可得,2yy′=6,即y′= ![]() ,
,
可得点A处的切线的斜率为 ![]() ,
,
则点A处切线的方程为 ![]() ,
,
令上式中y=0,得 ![]() ,
,
可得点B的坐标为 ![]() ,又
,又 ![]() ,
,
所以 ![]() ,
,
所以 ![]() ,所以FA∥BE,又AE∥FB,
,所以FA∥BE,又AE∥FB,
故四边形AEBF为平行四边形,
再由抛物线的定义,得AF=AE,
所以四边形AEBF为菱形.

【解析】(1)求得抛物线的焦点坐标和准线方程,运用抛物线的定义可得点 ![]() 在线段OF的中垂线上,可得p=3,进而得到抛物线的方程;(2)四边形AEBF为菱形.由抛物线的对称性,设点
在线段OF的中垂线上,可得p=3,进而得到抛物线的方程;(2)四边形AEBF为菱形.由抛物线的对称性,设点 ![]() 在x轴的上方,求出抛物线的切线的斜率和切线的方程,令y=0,求得B的坐标,E,F的坐标,由向量相等即可得到四边形的形状.
在x轴的上方,求出抛物线的切线的斜率和切线的方程,令y=0,求得B的坐标,E,F的坐标,由向量相等即可得到四边形的形状.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a、b、c,已知向量 ![]() =(cosA,cosB),
=(cosA,cosB), ![]() =(a,2c﹣b),且
=(a,2c﹣b),且 ![]() ∥
∥ ![]() .
.
(1)求角A的大小;
(2)若a=4,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ax2+bx,(a,b∈R).
(1)设a=1,f(x)在x=1处的切线过点(2,6),求b的值;
(2)设b=a2+2,求函数f(x)在区间[1,4]上的最大值;
(3)定义:一般的,设函数g(x)的定义域为D,若存在x0∈D,使g(x0)=x0成立,则称x0为函数g(x)的不动点.设a>0,试问当函数f(x)有两个不同的不动点时,这两个不动点能否同时也是函数f(x)的极值点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD= ![]() ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.

(1) 求直线PB与平面POC所成角的余弦值;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,x轴被曲线C2:y=x2-b截得的线段长度等于C1的短轴长.已知C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,直线MA,MB分别与C1相交于点D,E.
,x轴被曲线C2:y=x2-b截得的线段长度等于C1的短轴长.已知C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,直线MA,MB分别与C1相交于点D,E.
(1)求C1,C2的方程;
(2)求证:MA⊥MB;
(3)记△MAB,△MDE的面积分别为S1,S2,若![]() ,求λ的取值范围.
,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示:

从甲城市2016年9月份的30天中随机抽取15天,这15天的PM2.5的日均浓度指数数据如茎叶图所示.
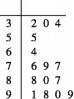
(1)试估计甲城市在2016年9月份的30天中,空气质量类别为优或良的天数;
(2)从甲城市的这15个监测数据中任取2个,设X是空气质量类别为优或良的天数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 为定义域
为定义域![]() 上单调函数,且存在区间
上单调函数,且存在区间![]() (其中
(其中![]() ),使得当
),使得当![]() 时,
时,![]() 的取值范围恰为
的取值范围恰为![]() ,则称函数
,则称函数![]() 是
是![]() 上的正函数,区间
上的正函数,区间![]() 叫做等域区间.
叫做等域区间.
(1)已知![]() 是
是![]() 上的正函数,求
上的正函数,求![]() 的等域区间;
的等域区间;
(2)试探究是否存在实数![]() ,使得函数
,使得函数![]() 是
是![]() 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=2,an+1=4an-3n+1,n∈N*.
(1)求证:数列{an-n}是等比数列;
(2)求数列{an}的前n项和Sn;
(3)求证:不等式Sn+1≤4Sn对任意n∈N*皆成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},其前n项和为Sn .
(1)若{an}是公差为d(d>0)的等差数列,且{ ![]() }也为公差为d的等差数列,求数列{an}的通项公式;
}也为公差为d的等差数列,求数列{an}的通项公式;
(2)若数列{an}对任意m,n∈N* , 且m≠n,都有 ![]() =am+an+
=am+an+ ![]() ,求证:数列{an}是等差数列.
,求证:数列{an}是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com