
如图,已知抛物线 :
: 和⊙
和⊙ :
: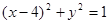 ,过抛物线
,过抛物线 上一点
上一点 作两条直线与⊙
作两条直线与⊙ 相切于
相切于 、
、 两点,分别交抛物线于
两点,分别交抛物线于 两点,圆心点
两点,圆心点 到抛物线准线的距离为
到抛物线准线的距离为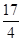 .
.

(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)当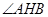 的角平分线垂直
的角平分线垂直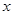 轴时,求直线
轴时,求直线 的斜率;
的斜率;
(Ⅲ)若直线 在
在 轴上的截距为
轴上的截距为 ,求
,求 的最小值.
的最小值.
(Ⅰ)抛物线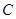 的方程为
的方程为 .(Ⅱ)
.(Ⅱ)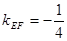 .
.
(Ⅲ)当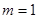 时,
时,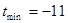 .
.
【解析】(1)求出圆心坐标,抛物线的准线方程,由圆心到准线的距离可求出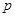 ,就得到抛物线的方程;(2)当
,就得到抛物线的方程;(2)当 的角平分线垂直
的角平分线垂直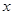 轴时,可得点
轴时,可得点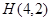 ,
, 的斜率与
的斜率与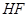 的斜率互为相反数.设出
的斜率互为相反数.设出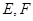 的坐标,表示出
的坐标,表示出 的斜率与
的斜率与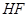 的斜率,和点
的斜率,和点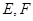 在抛物线上,即可求出
在抛物线上,即可求出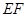 的斜率.(3)设出
的斜率.(3)设出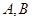 的坐标,由
的坐标,由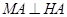 可得
可得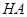 的斜率,可写出
的斜率,可写出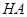 的方程,同理得
的方程,同理得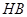 的方程.就得到
的方程.就得到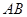 的方程.令
的方程.令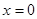 ,可得
,可得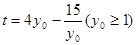 ,求出函数的值域即得到
,求出函数的值域即得到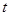 的最小值.
的最小值.
(Ⅰ)∵点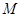 到抛物线准线的距离为
到抛物线准线的距离为
 ,
,
∴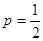 ,即抛物线
,即抛物线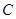 的方程为
的方程为 .····························································· 2分
.····························································· 2分
(Ⅱ)法一:∵当 的角平分线垂直
的角平分线垂直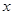 轴时,点
轴时,点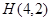 ,∴
,∴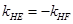 ,
,
设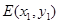 ,
,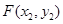 ,
,
∴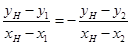 ,∴
,∴ 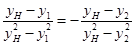 ,
,
∴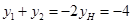 . ··················································································· 5分
. ··················································································· 5分
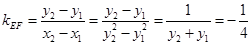 .··························································· 7分
.··························································· 7分
法二:∵当 的角平分线垂直
的角平分线垂直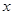 轴时,点
轴时,点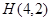 ,∴
,∴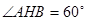 ,可得
,可得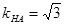 ,
, ,∴直线
,∴直线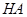 的方程为
的方程为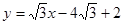 ,
,
联立方程组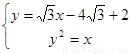 ,得
,得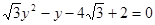 ,
,
∵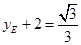 ,
,
∴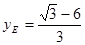 ,
,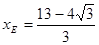 .······································································ 5分
.······································································ 5分
同理可得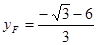 ,
,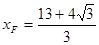 ,∴
,∴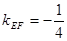 .································· 7分
.································· 7分
(Ⅲ)法一:设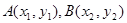 ,∵
,∵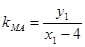 ,∴
,∴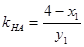 ,
,
可得,直线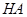 的方程为
的方程为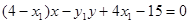 ,
,
同理,直线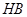 的方程为
的方程为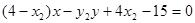 ,
,
∴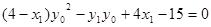 ,
,
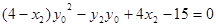 ,································································· 9分
,································································· 9分
∴直线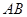 的方程为
的方程为 ,
,
令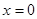 ,可得
,可得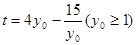 ,
,
∵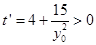 ,∴
,∴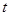 关于
关于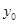 的函数在
的函数在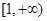 上单调递增,
上单调递增,
∴当 时,
时,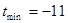 .·············································································· 12分
.·············································································· 12分
法二:设点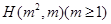 ,
,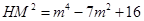 ,
,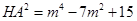 .
.
以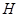 为圆心,
为圆心,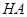 为半径的圆方程为
为半径的圆方程为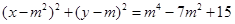 ,·· ①
,·· ①
⊙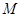 方程:
方程: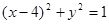 .······················ ②
.······················ ②
①-②得:
直线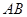 的方程为
的方程为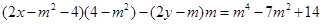 .·············· 9分
.·············· 9分
当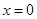 时,直线
时,直线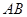 在
在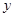 轴上的截距
轴上的截距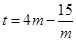
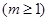 ,
,
∵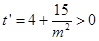 ,∴
,∴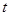 关于
关于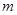 的函数在
的函数在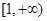 上单调递增,
上单调递增,
∴当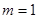 时,
时,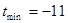 . 12分
. 12分


科目:高中数学 来源:2013-2014学年河北省高三上学期四调考试理科数学试卷(解析版) 题型:解答题
如图,已知抛物线 :
: 和⊙
和⊙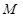 :
: ,过抛物线
,过抛物线 上一点
上一点 作两条直线与⊙
作两条直线与⊙ 相切于
相切于 、
、 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点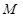 到抛物线准线的距离为
到抛物线准线的距离为 .
.

(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)当 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线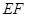 的斜率;
的斜率;
(Ⅲ)若直线 在
在 轴上的截距为,求的最小值.
轴上的截距为,求的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三上学期四调考试文科数学试卷(解析版) 题型:解答题
如图,已知抛物线 :
: 和⊙
和⊙ :
: ,过抛物线
,过抛物线 上一点
上一点 作两条直线与⊙
作两条直线与⊙ 相切于
相切于 、
、 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点 到抛物线准线的距离为
到抛物线准线的距离为 .
.

(1)求抛物线 的方程;
的方程;
(2)当 的角平分线垂直轴时,求直线
的角平分线垂直轴时,求直线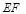 的斜率;
的斜率;
(3)若直线 在
在 轴上的截距为,求的最小值.
轴上的截距为,求的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省德州市高三上学期1月月考考试理科数学试卷(解析版) 题型:解答题
如图,已知抛物线 :
: 和⊙
和⊙ :
: ,过抛物线
,过抛物线 上一点
上一点 作两条直线与⊙
作两条直线与⊙ 相切于
相切于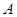 、
、 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点 到抛物线准线的距离为
到抛物线准线的距离为 .
.

(1)求抛物线 的方程;
的方程;
(2)当 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线 的斜率;
的斜率;
(3)若直线 在
在 轴上的截距为,求的最小值.
轴上的截距为,求的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知抛物线![]() :
:![]() 和⊙
和⊙![]() :
:![]() ,过抛物线
,过抛物线![]() 上一点
上一点
![]() 作两条直线与⊙
作两条直线与⊙![]() 相切于
相切于![]() 、
、![]() 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点![]() 到抛物线准线的距离为
到抛物线准线的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当![]() 的角平分线垂直
的角平分线垂直![]() 轴时,求直线
轴时,求直线![]() 的斜率.
的斜率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com