
| A. | $\frac{{\sqrt{3}}}{2}-\frac{1}{2}i$ | B. | $\frac{{\sqrt{3}}}{2}+\frac{1}{2}i$ | C. | $\sqrt{3}-i$ | D. | $\sqrt{3}+i$ |
分析 直接由复数代数形式的乘除运算化简复数z,则复数z的共扼复数可求.
解答 解:由z=$\frac{{1+\sqrt{3}i}}{{\sqrt{3}+i}}$=$\frac{(1+\sqrt{3}i)(\sqrt{3}-i)}{(\sqrt{3}+i)(\sqrt{3}-i)}=\frac{2\sqrt{3}+2i}{4}=\frac{\sqrt{3}+i}{2}$=$\frac{\sqrt{3}}{2}+\frac{1}{2}i$,
得$\overline{z}=\frac{\sqrt{3}}{2}-\frac{1}{2}i$.
故选:A.
点评 本题考查了复数代数形式的乘除运算,考查了共扼复数的求法,是基础题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
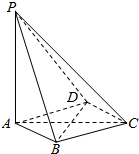 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2±$\sqrt{2}$ | B. | 2±2$\sqrt{2}$ | C. | 1±$\sqrt{2}$ | D. | $\sqrt{2}$±1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2n-1)2 | B. | $\frac{1}{3}({2^n}-1)$ | C. | $\frac{1}{3}(4-\frac{1}{{{4^{n-1}}}})$ | D. | $\frac{1}{3}({4^n}-1)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com