Rt△ABC的斜边AB在平面a内,且平面ABC和平面a所成二面角为60°,若直角边AC和平面a成角45°,则BC和平面a所成角为________.
30°
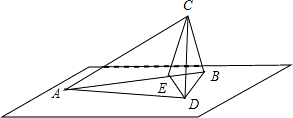
分析:过点C做CD垂直平面a,CE垂直AB,连接AD,BD,CE,DE,根据平面ABC和平面a所成二面角为60°,若直角边AC和平面a成角45°,结合直角三角形两直角边之积等于斜边与斜边上高,求出BC,CD的关系,进而求出BC和平面a所成角.
解答:过点C做CD垂直平面a,CE垂直AB,连接AD,BD,CE,DE
设CD=h,如图所示:
∵平面ABC和平面a所成二面角为60°,若直角边AC和平面a成角45°,
易得∠CED=60°,∠CAD=45°
则AC=

h,CE=
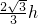
设BC=a,则∵BC•AC=AB•CE得:
BC=2h
故sin∠CBD=

故∠CBD=30°
故答案为:30°
点评:本题考查的知识点是直线与平面所成的角,其中求出BC和平面a所成角的三角函数的值是解答本题的关键.


 h,CE=
h,CE=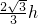



 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案