
【题目】设![]() ,函数
,函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若![]() 无零点,求实数
无零点,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 有两个相异零点
有两个相异零点![]() ,
, ![]() ,求证:
,求证: ![]()
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)根据导数几何意义得切线斜率为![]() ,再根据点斜式求切线方程(2)由于无零点,且函数恒有负值,所以函数最大值必小于零,根据导数可得函数最值,即得实数
,再根据点斜式求切线方程(2)由于无零点,且函数恒有负值,所以函数最大值必小于零,根据导数可得函数最值,即得实数![]() 的取值范围;也可先变量分离,根据两函数交点情况求实数
的取值范围;也可先变量分离,根据两函数交点情况求实数![]() 的取值范围(3)利用分析法证不等式,要证
的取值范围(3)利用分析法证不等式,要证![]() ,只要证
,只要证![]() ,根据零点条件可得
,根据零点条件可得![]() ,令
,令![]() ,构造函数
,构造函数![]() ,
, ![]() ,利用导数可得
,利用导数可得![]() 单调性,即得
单调性,即得![]() ,逆推可得结论
,逆推可得结论
试题解析:(1)函数的定义域为![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,则切线方程为
,则切线方程为![]() ,
,
即![]() .
.
(2)①若![]() 时,则
时,则![]() ,
, ![]() 是区间
是区间![]() 上的增函数,
上的增函数,
∵![]() ,
, ![]() ,
,
∴![]() ,函数
,函数![]() 在区间
在区间![]() 有唯一零点;
有唯一零点;
②若![]() ,
, ![]() 有唯一零点
有唯一零点![]() ;
;
③若![]() ,令
,令![]() ,得
,得![]() ,
,
在区间![]() 上,
上, ![]() ,函数
,函数![]() 是增函数;
是增函数;
在区间![]() 上,
上, ![]() ,函数
,函数![]() 是减函数;
是减函数;
故在区间![]() 上,
上, ![]() 的极大值为
的极大值为![]() ,
,
由于![]() 无零点,须使
无零点,须使![]() ,解得
,解得![]() ,
,
故所求实数![]() 的取值范围是
的取值范围是![]() .
.
(3)要证![]() ,两边同时取自然对数得
,两边同时取自然对数得![]() .
.
由![]() 得
得![]() ,得
,得![]() .
.
所以原命题等价于证明![]() .
.
因为![]() ,故只需证
,故只需证![]() ,即
,即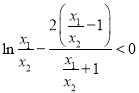 .
.
令![]() ,则
,则![]() ,设
,设![]() (
(![]() ),只需证
),只需证![]() .
.
而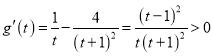 ,故
,故![]() 在
在![]() 单调递增,所以
单调递增,所以![]() .
.
综上得![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.
(1)证明:直线OM的斜率与l的斜率的乘积为定值;
(2)若l过点( ![]() ,m),延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率;若不能,说明理由.
,m),延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,a2+a7=﹣23,a3+a8=﹣29. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an+bn}是首项为1,公比为c的等比数列,求{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的个数为:( )
①y= ![]() 的图象关于(0,0)对称;
的图象关于(0,0)对称;
②y=x3+x+1的图象关于(0,1)对称;
③y= ![]() 的图象关于直线x=0对称;
的图象关于直线x=0对称;
④y=sinx+cosx的图象关于直线x= ![]() 对称.
对称.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[﹣2,0]时,f(x)=( ![]() )x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围是( )
)x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围是( )
A.( ![]() ,2)
,2)
B.( ![]() ,2)
,2)
C.[ ![]() ,2)
,2)
D.( ![]() ,2]
,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券类稳健型产品的收益与投资额成正比,投资股票类风险型产品的收益与投资额的算术平方根成正比,已知两类产品各投资1万元时的收益分别为0.125万元和0.5万元,如图:
(Ⅰ)分别写出两类产品的收益y(万元)与投资额x(万元)的函数关系;
(Ⅱ)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,最大收益是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com