练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设函数f（x）=3x+3-x，g（x）=3x-3-x的定义域均为R，则（　　）
    A、f（x）与g（x），均为奇函数
    B、f（x）与g（x）均为偶函数
    C、f（x）为奇函数，g（x）为偶函数
    D、f（x）为偶函数，g（x）为奇函数
    考点：函数奇偶性的判断,函数的定义域及其求法
    专题：函数的性质及应用
    分析：本题直接根据函数的奇偶性，判断出函数f（x）、g（x）的奇偶性，得到本题结论．
    解答： 解：∵定义在R上的函数f（x）=3x+3-x，
    ∴f（-x）=3-x+3x=f（x），
    ∴f（x）偶函数；
    ∵定义在R上的函数g（x）=3x-3-x
    ∴g（-x）=3-x-3x=-g（x），
    ∴g（x）是奇函数．
    故选D．
    点评：本题考查了奇偶性，本题难度不大，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知f（x）=ex+2ax（a为常数），曲线y=f（x）在点（0，f（0））处的切线与直线x-y-3=0垂直．
    （Ⅰ）求a的值及函数f（x）的单调区间；
    （Ⅱ）证明：当x＞0时，ex＞x2；
    （Ⅲ）设F（x）=f（x）-ex+
    1
    3
    x3+mx2    +1，若F（x）在（1，3）上单调递减，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    袋中有五张卡片，其中红色卡片三张，标号分别为1，2，3；蓝色卡片两张，标号分别为1，2；从五张卡片中，任取两张，这两张卡片颜色不同且标号之和小于4的概率为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=cos2
    x
    2
    -sin2
    x
    2
    -sinx．
    （1）求f（x）的最小正周期及单调增区间；
    （2）当x0∈（0，
    π
    4
    ）且f（x0）=
    4
    		2
    5
    时，求f（x0+
    π
    4
    ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=ex（ax+b）+x2+2x，曲线y=f（x）经过点P（0，1），且在点P处的切线为l：y=4x+1．
    （I）求a，b的值；
    （Ⅱ）若存在实数k，使得x∈[-2，-1]时f（x）≥x2+2（k+1）x+k恒成立，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

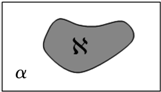    假定平面内的一条直线将该平面内的一个区域分成面积相等的两个区域，则称这条直线平分这个区域．如图，?是平面α内的任意一个封闭区域．现给出如下结论：
    ①过平面内的任意一点至少存在一条直线平分区域?；
    ②过平面内的任意一点至多存在一条直线平分区域?；
    ③区域?内的任意一点至少存在两条直线平分区域?；
    ④平面内存在互相垂直的两条直线平分区域?成四份．
    其中正确结论的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a，b均为正实数，若ab（a+b）=1，则a2+ab+4b的最小值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）是定义在R上的奇函数，f（3）=0，且x＜0时，xf′（x）＜f（x），则不等式f（x）≥0的解集是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知角α终边经过点P（12，-5），则sinα=
     
    ．

    查看答案和解析>>

    同步练习册答案