
设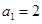 ,
,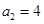 ,数列
,数列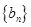 满足:
满足: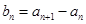 ,
,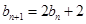 .
.
(Ⅰ)求证数列 是等比数列(要指出首项与公比);
是等比数列(要指出首项与公比);
(Ⅱ)求数列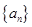 的通项公式.
的通项公式.
(Ⅰ)由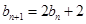 ,得
,得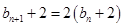 ,所以
,所以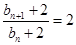
又因为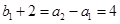 ,所以数列
,所以数列 是首项为4,公比为2的等比数列.
是首项为4,公比为2的等比数列.
(Ⅱ)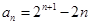 .
.
解析试题分析:(Ⅰ)当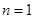 时,由题意得
时,由题意得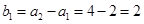 ,所以数列
,所以数列 的首项为
的首项为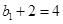 ,由等比数列定义知,若证数列
,由等比数列定义知,若证数列 为等比数列,则需要证明
为等比数列,则需要证明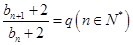 ,其中公比
,其中公比 为常数,为此只须将等式
为常数,为此只须将等式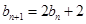 两边同时加上2可得
两边同时加上2可得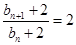 ,此时公比
,此时公比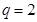 ,从而证明数列
,从而证明数列 是等比数列;( Ⅱ)由(Ⅰ)可得数列
是等比数列;( Ⅱ)由(Ⅰ)可得数列 的通项公式为
的通项公式为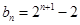 ,再由等式
,再由等式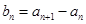 ,可得
,可得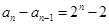 ,此时有
,此时有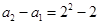 ,
,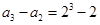 , ,
, , 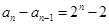 ,将上列式子两边相加可得
,将上列式子两边相加可得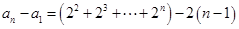 ,即
,即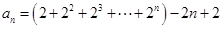 ,再由等比数列前
,再由等比数列前 项和公式,可得出数列
项和公式,可得出数列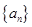 的通项公式(叠加消项法在求数列的通项、前
的通项公式(叠加消项法在求数列的通项、前 项和中常常用到,其特点是根据等式两边结构特征,一边相加可消掉中间项,另一边相加可以得到某一特殊数列或是常数).
项和中常常用到,其特点是根据等式两边结构特征,一边相加可消掉中间项,另一边相加可以得到某一特殊数列或是常数).
试题解析:(Ⅰ)由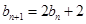 ,得
,得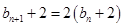 ,所以
,所以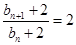 4分
4分
又因为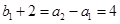 ,所以数列
,所以数列 是首项为4,公比为2的等比数列. 6分
是首项为4,公比为2的等比数列. 6分
(Ⅱ)由(Ⅰ)知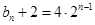 ,则
,则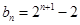 ,所以
,所以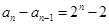 . 8分
. 8分
令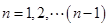 ,叠加得
,叠加得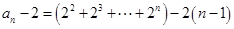 ,
,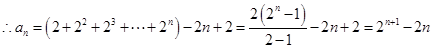 12分
12分
考点:1.等比数列定义;2.数列的通项公式.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
已知数列{an}的前n项和为Sn,且Sn=2an-1;数列{bn}满足bn-1-bn=bnbn-1(n≥2,n∈N*),b1=1.
(1)求数列{an},{bn}的通项公式;
(2)求数列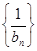 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知各项均为正数的数列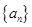 的前
的前 项和为
项和为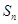 ,数列
,数列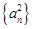 的前
的前 项和为
项和为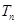 ,且
,且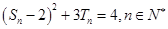 .
.
⑴证明:数列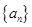 是等比数列,并写出通项公式;
是等比数列,并写出通项公式;
⑵若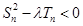 对
对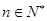 恒成立,求
恒成立,求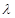 的最小值;
的最小值;
⑶若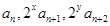 成等差数列,求正整数
成等差数列,求正整数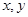 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知各项均不相等的等差数列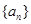 的前三项和为18,
的前三项和为18,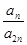 是一个与
是一个与 无关的常数,若
无关的常数,若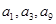 恰为等比数列
恰为等比数列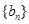 的前三项,
的前三项,
(1)求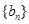 的通项公式.
的通项公式.
(2)记数列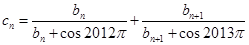 ,
,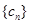 的前三
的前三 项和为
项和为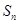 ,求证:
,求证: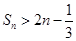
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com