
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在![]() 内的产品为合格品,否则为不合格品,统计结果如表:
内的产品为合格品,否则为不合格品,统计结果如表:
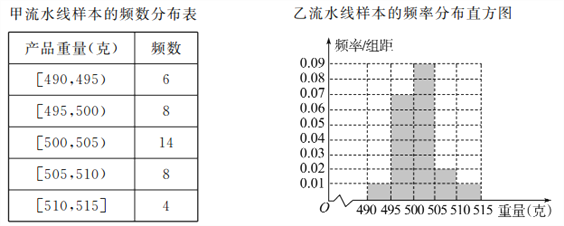
(Ⅰ)求甲流水线样本合格的频率;
(Ⅱ)从乙流水线上重量值落在![]() 内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
【答案】(Ⅰ)0.75; (Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)首先计算落在![]() 的频数,频数除以样本容量就是频率;(Ⅱ)根据频率分布直方图计算
的频数,频数除以样本容量就是频率;(Ⅱ)根据频率分布直方图计算![]() 和
和![]() 的频数,并且对产品编号,列举任选两件的基本事件,和恰有一件合格的基本事件的个数,计算其概率.
的频数,并且对产品编号,列举任选两件的基本事件,和恰有一件合格的基本事件的个数,计算其概率.
试题解析:(Ⅰ)由表知甲流水线样本中合格品数为![]() ,
,
故甲流水线样本中合格品的频率为![]() .
.
(Ⅱ)乙流水线上重量值落在![]() 内的合格产品件数为
内的合格产品件数为![]() ,
,
不合格产品件数为![]() .
.
设合格产品的编号为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,不合格产品的编号为
,不合格产品的编号为![]() ,
, ![]() .
.
抽取2件产品的基本事件空间为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共15个.
共15个.
用![]() 表示“2件产品恰好只有一件合格”这一基本事件,则
表示“2件产品恰好只有一件合格”这一基本事件,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共8个,
共8个,
故所求概率![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=log4(4x+1)+ax(a∈R).
(1)若函数f(x)是定义在R上的偶函数,求a的值;
(2)若不等式f(x)+f(﹣x)≥mt+m对任意x∈R,t∈[﹣2,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
为庆祝“2017年中国长春国际马拉松赛”,某单位在庆祝晚会中进行嘉宾现场抽奖活动.抽奖盒中装有大小相同的6个小球,分别印有“长春马拉松”和“美丽长春”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“长春马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取3次.已知从盒中抽取两个小球不都是“美丽长春”标志的概率为![]() .
.
(Ⅰ)求盒中印有“长春马拉松”标志的小球个数;
(Ⅱ)用η表示某位嘉宾抽奖的次数,求η的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF= ![]() ,给出下列结论:
,给出下列结论:
(1)AC⊥BE;
(2)EF∥平面ABCD;
(3)三棱锥A﹣BEF的体积为定值;
(4)异面直线AE,BF所成的角为定值.
其中错误的结论有( )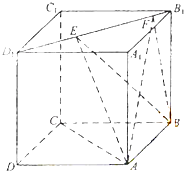
A.0个
B.1 个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王府井百货分店今年春节期间,消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对春节前7天参加抽奖活动的人数进行统计, ![]() 表示第
表示第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断变量![]() 与
与![]() 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若该活动只持续10天,估计共有多少名顾客参加抽奖.
参与公式:  ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,sinC+sin(A﹣B)=3sin2B.若 ![]() ,则
,则 ![]() =( )
=( )
A.![]()
B.3
C.![]() 或3
或3
D.3或 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com