
图是一个几何体的三视图,根据图中数据,可得该几何体的表面积、体积分别是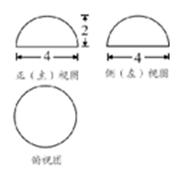
A.32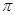 、 、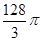 | B.16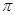 、 、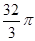 |
C.12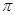 、 、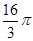 | D.8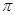 、 、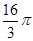 |
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:单选题
直三棱柱ABC-A B
B C
C 中 ,若∠BAC=90°,AB=AC=AA
中 ,若∠BAC=90°,AB=AC=AA ,则异面直线BA
,则异面直线BA 与AC
与AC 所成的角等于 ( )
所成的角等于 ( )
| A.60° | B.45° | C.30° | D.90° |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
我国齐梁时代的数学家祖暅(公元前5-6世纪)提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.
设:由曲线 和直线
和直线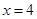 ,
,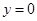 所围成的平面图形,绕
所围成的平面图形,绕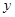 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为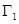 ;由同时满足
;由同时满足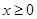 ,
,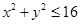 ,
,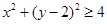 ,
,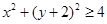 的点
的点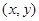 构成的平面图形,绕
构成的平面图形,绕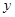 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察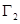 可以得到
可以得到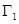 的体积为
的体积为
A.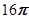 | B.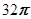 | C.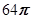 | D.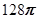 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com