
【题目】已知函数![]() (
(![]() )的图象为曲线
)的图象为曲线![]() .
.
(Ⅰ)求曲线![]() 上任意一点处的切线的斜率的取值范围;
上任意一点处的切线的斜率的取值范围;
(Ⅱ)若曲线![]() 上存在两点处的切线互相垂直,求其中一条切线与曲线
上存在两点处的切线互相垂直,求其中一条切线与曲线![]() 的切点的横坐标的取值范围;
的切点的横坐标的取值范围;
(Ⅲ)试问:是否存在一条直线与曲线C同时切于两个不同点?如果存在,求出符合条件的所有直线方程;若不存在,说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某公司组织开展“学习强国”的学习活动,活动第一周甲、乙两个部门员工的学习情况统计如下:
学习活跃的员工人数 | 学习不活跃的员工人数 | |
甲 | 18 | 12 |
乙 | 32 | 8 |
(1)从甲、乙两个部门所有员工中随机抽取1人,求该员工学习活跃的概率;
(2)根据表中数据判断能否有![]() 的把握认为员工学习是否活跃与部门有关;
的把握认为员工学习是否活跃与部门有关;
(3)活动第二周,公司为检查学习情况,从乙部门随机抽取2人,发现这两人学习都不活跃,能否认为乙部门第二周学习的活跃率比第一周降低了?
参考公式: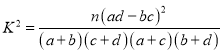 ,其中
,其中![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求曲线C的普通方程;
(2)直线l的参数方程为![]() ,(t为参数),直线l与x轴交于点F,与曲线C的交点为A,B,当
,(t为参数),直线l与x轴交于点F,与曲线C的交点为A,B,当![]() 取最小值时,求直线l的直角坐标方程.
取最小值时,求直线l的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—5: 不等式选讲
已知函数f(x)=![]() 的定义域为R.
的定义域为R.
(Ⅰ)求实数m的取值范围;
(Ⅱ)若m的最大值为n,当正数a,b满足![]() =n时,求7a+4b的最小值.
=n时,求7a+4b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD–A1B1C1D1中,已知底面ABCD是菱形,点P是侧棱C1C的中点.

(1)求证:AC1∥平面PBD;
(2)求证:BD⊥A1P.
查看答案和解析>>
科目:高中数学 来源: 题型:
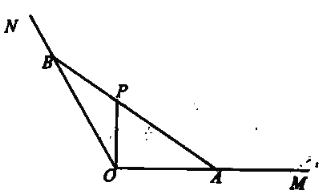
【题目】如图所示,某海滨养殖场有一块可用水城,该养殖场用隔离网![]() 把该水域分为两个部分,其中
把该水域分为两个部分,其中![]() 百米,现计划过
百米,现计划过![]() 处再修建一条直线型隔离网,其端点分别在
处再修建一条直线型隔离网,其端点分别在![]() 上,记为
上,记为![]()
(1)若要使得所围区域![]() 面积不大于
面积不大于![]() 平方百米,求
平方百米,求![]() 的取值范围:
的取值范围:
(2)若要在![]() 区域内养殖鱼类甲,
区域内养殖鱼类甲,![]() 区域内养殖鱼类乙,已知鱼类甲的养殖成本是
区域内养殖鱼类乙,已知鱼类甲的养殖成本是![]() 万元/平方百米,鱼类乙的养殖成本是
万元/平方百米,鱼类乙的养殖成本是![]() 万元/平方百米.试确定
万元/平方百米.试确定![]() 的值,使得养殖成本最小,
的值,使得养殖成本最小,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆的方程;
(2)M,N是椭圆上关于x轴对称的两点,P是椭圆上不同于M,N的一点,直线PM,PN交x轴于D(xD,0)E(xE,0),证明:xDxE为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2﹣4ρsin(θ![]() )=0.
)=0.
(1)求曲线C的直角坐标方程;
(2)若直线l的参数方程是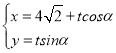 (α为参数),且α∈(
(α为参数),且α∈(![]() ,π)时,直线l与曲线C有且只有一个交点P,求点P的极径.
,π)时,直线l与曲线C有且只有一个交点P,求点P的极径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com