
 如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.
如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.分析 (1)证明:△PAC∽△PCB,可得$\frac{PC}{PB}=\frac{PA}{PC}=\frac{AC}{CB}$,即可证明PC2=PA,PB;
(2)若3AC=4BC,则$\frac{PC}{PB}$=$\frac{4}{3}$,利用切割线定理,求线段PC的长.
解答 (1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵AD⊥DC于D,且AC平分∠DAB,
∴∠PDA=90°,∠DAC=∠BAC,
∵∠PCA=∠PDA+∠DAC,∠PBC=∠ACB+∠BAC,
∴∠PCA=∠PBC,
∵∠BPC=∠CPA,
∴△PAC∽△PCB,
∴$\frac{PC}{PB}=\frac{PA}{PC}=\frac{AC}{CB}$,
∴PC2=PA•PB;
(2)解:∵3AC=4BC,∴$\frac{PC}{PB}$=$\frac{4}{3}$,
设PC=4k,PB=3k,则PA=3k+7,
∴(4k)2=3k(3k+7),
∴k=3(k=0舍去),
∴PC=12.
点评 本题考查三角形相似的判定与性质,考查切割线定理,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图:在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,且C1B1⊥AB.
如图:在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,且C1B1⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.
某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
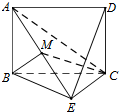 如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com