
【题目】已知![]() ,不等式
,不等式![]() 的解集是
的解集是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)不等式组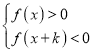 的正整数解只有一个,求实数k取值范围;
的正整数解只有一个,求实数k取值范围;
(3)若对于任意![]() ,不等式
,不等式![]() 恒成立,求t的取值范围.
恒成立,求t的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据不等式![]() 的解集是
的解集是![]() ,得到
,得到![]() 是一元二次方程
是一元二次方程![]() 的两个实数根,利用韦达定理得到参数所满足的条件,最后求得结果;
的两个实数根,利用韦达定理得到参数所满足的条件,最后求得结果;
(2)首先求得不等式组的解,根据只有一个正整数解,得到参数所满足的条件,求得结果;
(3)根据不等式恒成立,分类讨论,结合函数图象的特征求得结果.
(1)因为不等式![]() 的解集是
的解集是![]() ,
,
所以![]() 是一元二次方程
是一元二次方程![]() 的两个实数根,
的两个实数根,
可得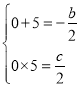 ,解得
,解得![]()
所以![]() ;
;
(2)不等式组![]() 即为,
即为,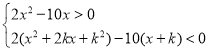 ,
,
解得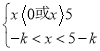 ,
,
因为不等式组的正整数解只有一个,可得该正整数解就是6,
可得![]() ,解得
,解得![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() ;
;
(3)![]() ,即
,即![]() ,即
,即![]() ,
,
当![]() 时显然成立,
时显然成立,
当![]() 时,有
时,有![]() ,即
,即![]() ,
,
解得![]() ,所以
,所以![]() ,
,
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
所以只要其最大值满足条件即可,
所以有![]() ,解得
,解得![]() ,即
,即![]() ,
,
综上,![]() 的取值范围是
的取值范围是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某学生将语文、数学、英语、物理、化学、生物![]() 科的作业安排在周六、周日完成,要求每天至少完成两科,且数学、物理作业不在同一天完成,则完成作业的不同顺序种数为______.
科的作业安排在周六、周日完成,要求每天至少完成两科,且数学、物理作业不在同一天完成,则完成作业的不同顺序种数为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次考试中,某班级50名学生的成绩统计如下表,规定75分以下为一般,大于等于75分小于85分为良好,85分及以上为优秀.
分数 | 69 | 73 | 74 | 75 | 77 | 78 | 79 | 80 | 82 | 83 | 85 | 87 | 89 | 93 | 95 | 合计 |
人数 | 2 | 4 | 4 | 2 | 3 | 4 | 6 | 3 | 3 | 4 | 4 | 5 | 2 | 3 | 1 | 50 |
经计算,样本的平均值![]() ,标准差
,标准差![]() .为评判该份试卷质量的好坏,从其中任取一人,记其成绩为X,并根据以下不等式进行评判:
.为评判该份试卷质量的好坏,从其中任取一人,记其成绩为X,并根据以下不等式进行评判:
①![]() ;
;
②![]() ;
;
③![]() .
.
评判规则:若同时满足上述三个不等式,则被评为优秀试卷;若仅满足其中两个不等式,则被评为合格试卷;其他情况,则被评为不合格试卷.
(1)试判断该份试卷被评为哪种等级;
(2)按分层抽样的方式从3个层次的学生中抽出10名学生,再从抽出的10名学生中随机抽出4人进行学习方法交流,用随机变量表示4人中成绩优秀的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂加工产品![]() 的工人的年龄构成和相应的平均正品率如下表:
的工人的年龄构成和相应的平均正品率如下表:
年龄(单位:岁) |
|
|
|
|
人数比例 | 0.3 | 0.4 | 0.2 | 0.1 |
平均正品率 | 85% | 95% | 80% | 70% |
(1)画出该工厂加工产品![]() 的工人的年龄频率分布直方图;
的工人的年龄频率分布直方图;
(2)估计该工厂工人加工产品![]() 的平均正品率;
的平均正品率;
(3)该工厂想确定一个转岗年龄![]() 岁,到达这个年龄的工人不再加工产品
岁,到达这个年龄的工人不再加工产品![]() ,转到其他岗位,为了使剩余工人加工产品
,转到其他岗位,为了使剩余工人加工产品![]() 的平均正品率不低于90%,若年龄在同一区间内的工人加工产品
的平均正品率不低于90%,若年龄在同一区间内的工人加工产品![]() 的正品率都取相应区间的平均正品率,则估计
的正品率都取相应区间的平均正品率,则估计![]() 最高可定为多少岁?
最高可定为多少岁?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若S![]() 是公差不为0的等差数列
是公差不为0的等差数列![]() 的前
的前![]() 项和,且
项和,且![]() 成等比数列。
成等比数列。
(1)求等比数列![]() 的公比;
的公比;
(2)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)设![]() ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和,求使得
项和,求使得![]() 对所有
对所有![]() 都成立的最小正整数
都成立的最小正整数![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论:在回归分析中
(1)可用相关指数![]() 的值判断模型的拟合效果,
的值判断模型的拟合效果,![]() 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
(2)可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好;
(3)可用相关系数![]() 的值判断模型的拟合效果,
的值判断模型的拟合效果,![]() 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
(4)可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
以上结论中,不正确的是( )
A.(1)(3)B.(2)(3)C.(1)(4)D.(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实验中学从高二级部中选拔一个班级代表学校参加“学习强国知识大赛”,经过层层选拔,甲、乙两个班级进入最后决赛,规定回答1个相关问题做最后的评判选择由哪个班级代表学校参加大赛.每个班级6名选手,现从每个班级6名选手中随机抽取3人回答这个问题已知这6人中,甲班级有4人可以正确回答这道题目,而乙班级6人中能正确回答这道题目的概率每人均为![]() ,甲、乙两班级每个人对问题的回答都是相互独立,互不影响的.
,甲、乙两班级每个人对问题的回答都是相互独立,互不影响的.
(1)求甲、乙两个班级抽取的6人都能正确回答的概率;
(2)分别求甲、乙两个班级能正确回答题目人数的期望![]() 和方差
和方差![]() 、
、![]() ,并由此分析由哪个班级代表学校参加大赛更好?
,并由此分析由哪个班级代表学校参加大赛更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凤鸣山中学的高中女生体重![]() (单位:kg)与身高
(单位:kg)与身高![]() (单位:cm)具有线性相关关系,根据一组样本数据
(单位:cm)具有线性相关关系,根据一组样本数据![]() (
(![]() ),用最小二乘法近似得到回归直线方程为
),用最小二乘法近似得到回归直线方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.![]() 与
与![]() 具有正线性相关关系
具有正线性相关关系
B.回归直线过样本的中心点![]()
C.若该中学某高中女生身高增加1cm,则其体重约增加0.85kg
D.若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com