
【题目】在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在S市的A区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
x(个) | 2 | 3 | 4 | 5 | 6 |
y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间满足的关系式为:![]() ,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店,才能使A区平均每个分店的年利润最大?
,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店,才能使A区平均每个分店的年利润最大?
附:回归方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
![]()
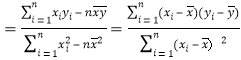 ,
,![]()
![]()
![]()
![]() .
.
(参考数据:![]() ,
,![]() )
)
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若同时满足下列三个条件:①
,若同时满足下列三个条件:① ![]() ;② 当
;② 当![]() ,且
,且![]() 时,都有
时,都有 ![]() ;③ 当
;③ 当![]() ,且
,且![]() 时,都有
时,都有![]() , 则称
, 则称![]() 为“偏对称函数”.现给出下列三个函数:
为“偏对称函数”.现给出下列三个函数: ![]() ;
; ![]() ;
; ![]() 则其中是“偏对称函数”的函数个数为
则其中是“偏对称函数”的函数个数为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的两个焦点分别为
的两个焦点分别为![]() ,点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
,点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
(1)求椭圆C的方程;
(2)过点M(1,0)的直线与椭圆C相交于A、B两点,设点N(3,2),记直线AN、BN的斜率分别为k1、k2,求证:k1+k2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下命题正确的是( )
A. 若直线![]() ,
,![]() ,
,![]() ,则直线a,b异面
,则直线a,b异面
B. 空间内任意三点可以确定一个平面
C. 空间四点共面,则其中必有三点共线
D. 直线![]() ,
,![]() ,
,![]() ,则直线a,b异面
,则直线a,b异面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域在![]() 上的函数
上的函数![]() 满足对于任意的
满足对于任意的![]() ,都有
,都有![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 成立.
成立.
(1)设![]() ,求证
,求证![]() ;
;
(2)设![]() ,若
,若![]() ,试比较x1与x2的大小;
,试比较x1与x2的大小;
(3)若![]() ,解关于x的不等式
,解关于x的不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日为庆祝中国人民共和国成立70周年在北京天安门广场举行了盛大的阅兵仪式,共有580台(套)装备、160余架各型飞机接受检阅,受阅装备均为中国国产现役主战装备,其中包括部分首次公开亮相的新型装备.例如,在无人作战第三方队中就包括了两型侦察干扰无人机,可以在遥控设备或自备程序控制操纵的情况下执行任务,进行对敌方通讯设施的电磁压制和干扰,甚至压制敌人的防空系统.某作战部门对某处的战场实施“电磁干扰”实验,据测定,该处的“干扰指数”与无人机干扰源的强度和距离之比成正比,比例系数为常数![]() (
(![]() ),现已知相距36
),现已知相距36![]() 的
的![]() 、
、![]() 两处配置两架无人机干扰源,其对敌干扰的强度分别为1和
两处配置两架无人机干扰源,其对敌干扰的强度分别为1和![]() (
(![]() ),它们连线段上任意一点
),它们连线段上任意一点![]() 处的干扰指数
处的干扰指数![]() 等于两机对该处的干扰指数之和,设
等于两机对该处的干扰指数之和,设![]() (
(![]() ).
).
(1)试将![]() 表示为
表示为![]() 的函数,指出其定义域;
的函数,指出其定义域;
(2)当![]() ,
,![]() 时,试确定“干扰指数”最小时
时,试确定“干扰指数”最小时![]() 所处位置.
所处位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,国家深入推进精准脱贫,加大资金投入,强化社会帮扶,为了更好的服务于人民,派调查组到某农村去考察和指导工作.该地区有200户农民,且都从事水果种植,据了解,平均每户的年收入为3万元.为了调整产业结构,调查组和当地政府决定动员部分农民从事水果加工,据估计,若能动员![]() 户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高
户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高![]() ,而从事水果加工的农民平均每户收入将为
,而从事水果加工的农民平均每户收入将为![]() 万元.
万元.
(1)若动员![]() 户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求
户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这200户农民中从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com