
����Ŀ��ij���߶����칫˾Ϊ��Ӧ���й�����2025��������ļ�֡���������������Ϊ�ȡ���ɫ��չ���ṹ�Ż����˲�Ϊ�����Ļ�������,���Ӵ��Ʒ�з�Ͷ��,�±��Ǹù�˾2017��5~12�·��з�����(����Ԫ)�Ͳ�Ʒ����(��̨)�ľ������ݣ�

��1)�������ݿ�֪![]() ��
��![]() ֮�����������ع�ϵ
֮�����������ع�ϵ
(i)���![]() ����
����![]() �����Իع鷽��(ϵ����ȷ��
�����Իع鷽��(ϵ����ȷ��![]() );
);
(ii)��2018��6�·��з�Ͷ��Ϊ25����Ԫ,������������Իع鷽�̹��Ƶ��²�Ʒ��������
(2)��˾��2017�������ܽ�ʱ���Ӹ���8~12�·���5�����г�ȡ3���µ����ݽ����ص����,��û�г鵽9�·����ݵĸ���.
�����: ![]() ��
��![]() .
.
�ο���ʽ:����һ������![]() ,
,![]() ,��ع�ֱ��
,��ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ:
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ: 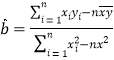 ��
��![]() .
.
���𰸡�(1)(i)![]() ;(2)6.415��̨.(2)
;(2)6.415��̨.(2)![]() .
.
��������������(1)(i)��������ϵ���ļ��㹫ʽ�ɵ����Իع鷽��Ϊ![]() .
.
(ii)�ɻع鷽�̿�Ԥ��²�Ʒ������Ϊ![]() ��̨.
��̨.
(2)�������֪�����е��¼�����![]() �ֻ����¼�,����������¼���
�ֻ����¼�,����������¼���![]() �ֻ����¼��������
�ֻ����¼��������![]() .
.
��⣺(1)(i)��Ϊ![]() ,
,
����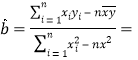
![]()
![]() ��
��
![]()
![]() ��
��
����![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() .
.
(ii)��![]() ʱ,
ʱ, ![]()
![]() (��̨).
(��̨).
(2)��![]() �·���
�·���![]() ���µ����ݷֱ�Ϊ
���µ����ݷֱ�Ϊ![]() ,���г�ȡ
,���г�ȡ![]() ���µ����л����¼���:
���µ����л����¼���: ![]()
![]() ,
,
��![]() �ֻ����¼�,
�ֻ����¼�,
û�г鵽![]() �·ݵ���
�·ݵ���![]()
![]() ��
��![]() �ֻ����¼���
�ֻ����¼���
���Ը���![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() .
.
������![]() ������
������![]() ���м�ֵ����ʵ��
���м�ֵ����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ��Ψһ�����
��Ψһ�����![]() ������
������![]() ��ֵ.��ע��
��ֵ.��ע��![]() Ϊȡ����������ʾ������
Ϊȡ����������ʾ������![]() �������������
�������������![]() ���������ݹ��ο���
���������ݹ��ο���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��![]() sin2x+sinxcosx+
sin2x+sinxcosx+![]() ��x��[0��
��x��[0��![]() ]
]
��1������f��x����ֵ��
��2����f��![]() ��=
��=![]() ��������0���У�����sin����ֵ��
��������0���У�����sin����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й������˵��������ǣ� ��
A.��p��qΪ�����⣬��p��q��Ϊ������
B.��x��1������x2��3x+2��0���ij�ֲ���Ҫ����
C.��������x2��3x+2��0����x��1�����������������x��1����x2��3x+2��0��
D.��������p��x��0��2x��3����VP��x��0��2x��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
(1)��![]() ,����
,����![]() �ڵ�
�ڵ�![]() �������������������ϵĽؾ�֮��Ϊ2,��
�������������������ϵĽؾ�֮��Ϊ2,��![]() ��ֵ
��ֵ
(2)�����������![]() �������
�������![]() ����
����![]() ����.��
����.��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������a��(sinx��1,1)��b��(sinx��3,1)��c��(��1����2)��d��(k,1)��k��R.
(1)��x��[��![]() ��
��![]() ]����a��(b��c)����x��ֵ��
]����a��(b��c)����x��ֵ��
(2)������x��R��ʹ��(a��d)��(b��c)����k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȫ��ͬ��3ֻ�����4ֻ����Ӵ��������ȡ��.
���������зŻص�ȡ3�Σ�ÿ��ȡһ������ȡ��2������1������ĸ��ʣ�
���������Żص�ȡ3�Σ�ÿ��ȡһ������ȡ��ÿֻ�����2�֣�ȡ��ÿֻ�����1�֣���÷�![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij�س�����һ�֡��������������߶���ɣ���ṹ��ʹ����������ˮƽ�������һ�����ڵ�ֱ����ֱ���ϣ�������ɸá������������ȳ����߶ι�����Ϊ![]() ������Ϊ
������Ϊ![]() ��
��

��1���ж�������![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��2����![]() ����
����![]() ��ͬһˮƽ����ʱ����
��ͬһˮƽ����ʱ����![]() ��ƽ��
��ƽ��![]() ���ɽǵĴ�С������÷����Ǻ���ֵ��ʾ����
���ɽǵĴ�С������÷����Ǻ���ֵ��ʾ����
��3�����á������ŵغ���ĸ��߶θ�����Ҫ���Ե��������ɽǵĴ�С���ұ��������߶������ɽ���ͬ����![]() ��
��![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��������������ֵ��
��������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��д�����и�������ɵġ�![]() ��
��![]() ������
������![]() ��
��![]() ���Լ�����
���Լ�����![]() ����ʽ�����⣬���ж����ǵ���٣�
����ʽ�����⣬���ж����ǵ���٣�
(1)![]() ��
��![]() ����������
����������![]() ��
��![]() ��������
��������
(2)![]() ������ʽ
������ʽ![]() �Ľ⼯��
�Ľ⼯��![]() ��
��![]() ������ʽ
������ʽ![]() �Ľ⼯��
�Ľ⼯��![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com