
【题目】判断下列各题中p是q的什么条件.
(1)p:|x|=|y|,q:x=y;
(2)p:△ABC是直角三角形,q:△ABC是等腰三角形;
(3)p:四边形的对角线互相平分,q:四边形是矩形;
(4)p:圆x2+y2=r2(r>0)与直线ax+by+c=0相切,q:c2=(a2+b2)r2.
【答案】见解析
【解析】
根据充要条件的定义,逐一判断四个小题中![]() 和
和![]() 的关系,可得结论.
的关系,可得结论.
(1)∵|x|=|y|不能推出x=y,但x=y |x|=|y|,∴p是q的必要不充分条件.
(2)∵△ABC是直角三角形不能推出△ABC是等腰三角形,
△ABC是等腰三角形也不能推出△ABC是直角三角形,
∴p是q的既不充分也不必要条件.
(3)∵四边形的对角线互相平分不能推出四边形是矩形,
四边形是矩形能推出四边形的对角线互相平分,
∴p是q的必要不充分条件.
(4)若圆x2+y2=r2(r>0)与直线ax+by+c=0相切,则圆心(0,0)到直线ax+by+c=0的距离等于r,即r=![]() ,
,
∴c2=(a2+b2)r2;
反过来,若c2=(a2+b2)r2,则![]() =r成立,
=r成立,
说明圆x2+y2=r2(r>0)的圆心(0,0)到直线ax+by+c=0的距离等于r,
即圆x2+y2=r2(r>0)与直线ax+by+c=0相切.故p是q的充要条件.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.
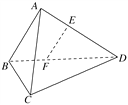
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A1B1C1D中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:

(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 为正方体,给出以下五个结论:
为正方体,给出以下五个结论:
① ![]() 平面
平面![]() ;
;
② ![]() ⊥平面
⊥平面![]() ;
;
③ ![]() 与底面
与底面![]() 所成角的正切值是
所成角的正切值是![]() ;
;
④ 二面角![]() 的正切值是
的正切值是![]() ;
;
⑤ 过点![]() 且与异面直线
且与异面直线![]() 和
和 ![]() 均成70°角的直线有4条.
均成70°角的直线有4条.
其中,所有正确结论的序号为________.
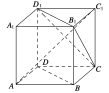
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上动点M到直线x=﹣1的距离比它到点F(2,0)的距离少1.
(1)求动点M的轨迹E的方程;
(2)已知点B(﹣1,0),设过点(1,0)的直线l与轨迹E交于不同的两点P、Q,证明:x轴是∠PBQ的角平分线所在的直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的参数方程为: ![]() (φ为参数),直线l的极坐标方程为ρ(cosθ+sinθ)=4.
(φ为参数),直线l的极坐标方程为ρ(cosθ+sinθ)=4.
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)若点P在曲线C上,点Q在直线l上,求线段PQ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(0,+∞)上的函数f(x)=a(x+ ![]() )﹣|x﹣
)﹣|x﹣ ![]() |(a∈R).
|(a∈R).
(1)当a= ![]() 时,求f(x)的单调区间;
时,求f(x)的单调区间;
(2)若f(x)≥ ![]() x对任意的x>0恒成立,求a的取值范围.
x对任意的x>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的![]() 倍和
倍和![]() 倍后,得到曲线
倍后,得到曲线![]()
(1)试写出曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求点
上求点![]() ,使得点
,使得点![]() 到直线
到直线![]() 的距离最大,并求距离最大值.
的距离最大,并求距离最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com