练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】“光明天使”基金收到甲乙丙三兄弟24万、25万、26万三笔捐款（一人捐一笔款），记者采访这三兄弟时，甲说：“乙捐的不是最少.”乙说：“甲捐的比丙多.”丙说：“若我捐的最少，则甲捐的不是最多.”根据这三兄弟的回答，确定乙捐了_________万.

    【答案】26

    【解析】

    根据三人的话进行推理可得．

    由甲乙两人的话知丙最小，再由丙的话知甲居中，因此乙最多为26万元．

    故答案为：26.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】一名工人维护3台独立的游戏机，一天内3台游戏机需要维护的概率分别为0.9、0.8和0.75，则一天内至少有一台游戏机不需要维护的概率为（ ）
    A.0.995
    B.0.54
    C.0.46
    D.0.005

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果奇函数f（x）在区间[1，5]上是减函数，且最小值3，那么f（x）在区间[﹣5，﹣1]上是（ ）
    A.增函数且最小值为3
    B.增函数最大值为3
    C.减函数且最小值为﹣3
    D.减函数且最大值为﹣3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知随机变量ξ服从正态分布N（0，σ2），P（ξ＞2）=0.023，则P（﹣2≤ξ≤2）=（ ）
    A.0.997
    B.0.954
    C.0.488
    D.0.477

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=lg（x2﹣2x﹣3）的定义域为集合A，函数g（x）=2x﹣a（x≤2）的值域为集合B． （Ⅰ）求集合A，B；
    （Ⅱ）已知命题p：m∈A，命题q：m∈B，若p是q的充分不必要条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设集合U={1，2，3，4，5}，集合A={1，2，3}，则UA=（ ）
    A.{1，2，3}
    B.{4，5}
    C.{1，2，3，4，5}
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知小明需从几门课程中选择一门作为自己的特长课程来学习，小明选完课后，同寝室的其他3位同学根据小明的兴趣爱好对小明选择的课程猜测如下：

    甲说：“小明选的不是篮球，选的是排球”；

    乙说：“小明选的不是排球，选的是书法”

    丙说：“小明选的不是排球，选的也不是现代舞”.

    已知3人中有1人说的全对，有1人说对了一半，另1人说的全不对，由此可推测小明选择的（ ）

    A.可能是书法B.可能是现代舞C.一定是排球D.可能是篮球

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场有甲、乙两种电子产品可供顾客选购．记事件A为“只买甲产品”，事件B为“至少买一种产品”，事件C为“至多买一种产品”，事件D为“不买甲产品”，事件E为“一种产品也不买”．判断下列事件是不是互斥事件，如果是，再判断它们是不是对立事件．
    （1）A与C；
    （2）B与E；
    （3）B与D；
    （4）B与C；
    （5）C与E.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，把两个全等的和分别置于平面直角坐标系中，使直角边在轴上，已知点，过两点的直线分别交轴、轴于点. 抛物线经过三点.

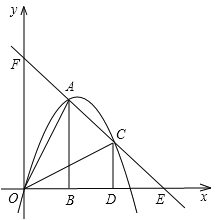
    （1）求该抛物线的函数解析式；

    （2）点为线段上的一个动点，过点作轴的平行线交抛物线于点，交轴于点，问是否存在这样的点，使得四边形为等腰梯形？若存在，求出此时点的坐标；若不存在，请说明理由；

    （3）若沿方向平移（点始终在线段上，且不与点重合），在平移的过程中与重叠部分的面积记为，试探究是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案