
若X是离散型随机变量,P(X=x1)= ,P(X=x2)=
,P(X=x2)= ,且x1<x2,又已知E(X)=
,且x1<x2,又已知E(X)= ,D(X)=
,D(X)= ,则x1+x2的值为( )
,则x1+x2的值为( )
(A) (B)
(B) (C)3 (D)
(C)3 (D)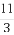
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:选择题
已知等差数列{an}中,|a3|=|a9|,公差d<0,Sn是数列{an}的前n项和,则( )
(A)S5>S6(B)S5<S6
(C)S6=0(D)S5=S6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:解答题
为缓解某路段交通压力,计划将该路段实施“交通限行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:
年龄 (岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频 数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成 人数 | 4 | 8 | 9 | 6 | 4 | 3 |
(1)作出被调查人员年龄的频率分布直方图.
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:填空题
抛掷两枚骰子,至少有一个4点或5点出现时,就说这次试验成功,则在10次试验中,成功次数X的期望是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十九选修4-5第一节练习卷(解析版) 题型:解答题
已知函数f(x)=|3x-6|-|x-4|.
(1)作出函数y=f(x)的图象;
(2)解不等式|3x-6|-|x-4|>2x.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十七选修4-4第一节练习卷(解析版) 题型:解答题
在极坐标系(ρ,θ)(0≤θ<2π)中,求曲线ρ=2sinθ与ρcosθ=1的交点Q的极坐标.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:解答题
本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分每小时收费标准为2元(不足1小时的部分按1小时计算)。有甲乙两人相互独立来该租车点租车骑游(各租一车一次),设甲、乙不超过两小时还车的概率分别为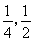 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为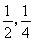 ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求出甲、乙两人所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量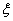 ,求
,求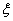 的分布列与数学期望
的分布列与数学期望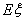 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com