
【题目】如下图,三棱柱![]() 中,侧面
中,侧面![]()
![]() 底面
底面![]() ,
, ![]() ,且
,且![]() ,O为
,O为![]() 中点.
中点.
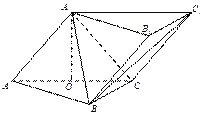
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦;
所成角的正弦;
(Ⅲ)在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点![]() 的位置.
的位置.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() 为
为![]() 的中点.
的中点.
【解析】(1)因为侧面![]() 底面
底面![]() ,所以只需证明
,所以只需证明![]() 即可.
即可.
(2)可以以O为原点,ON,OC,OA1所在直线为x,y,z轴建立空间直角坐标系,然后用向量的方法求解线面角的问题.
(3)在(2)的基础上也可以用向量来求点E位置.也可以取BC的中点M,连接OM,取BC1的中点E,连接ME,则OM//AB,ME//BB1//AA1,所以平面OMB//平面AA1B,所以OE//平面![]() .从而确定E为BC1的中点.
.从而确定E为BC1的中点.
(Ⅰ)证明:因为![]() ,且O为AC的中点,
,且O为AC的中点,
所以![]()
又由题意可知,平面![]() 平面
平面![]() ,交线为
,交线为![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(Ⅱ)如图,以O为原点, ![]() 所在直线分别为x,y,z轴建立空间直角坐标系.
所在直线分别为x,y,z轴建立空间直角坐标系.
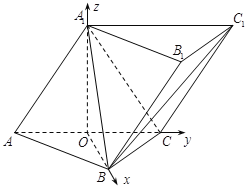
由题意可知, ![]() 又
又![]()
![]()
所以得: ![]()
则有: ![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有
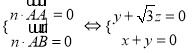 ,令
,令![]() ,得
,得![]()
所以![]()
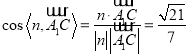
因为直线![]() 与平面
与平面![]() 所成角
所成角![]() 和向量
和向量![]() 与
与![]() 所成锐角互余,所以
所成锐角互余,所以![]()
(Ⅲ)设![]()
即![]() ,得
,得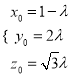
所以![]() 得
得![]()
令![]() 平面
平面![]() ,得
,得![]() ,
,
即![]() 得
得![]()
即存在这样的点E,E为![]() 的中点
的中点


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知单调递增的等差数列{an},满足|a10a11|>a10a11 , 且a102<a112 , Sn为其前n项和,则( )
A.a8+a12>0
B.S1 , S2 , …S19都小于零,S10为Sn的最小值
C.a8+a13<0
D.S1 , S2 , …S20都小于零,S10为Sn的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程![]() ,其左焦点、上顶点和左顶点分别为
,其左焦点、上顶点和左顶点分别为![]() ,
, ![]() ,
, ![]() ,坐标原点为
,坐标原点为![]() ,且线段
,且线段![]() ,
, ![]() ,
, ![]() 的长度成等差数列.
的长度成等差数列.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若过点![]() 的一条直线
的一条直线![]() 交椭圆于点
交椭圆于点![]() ,
, ![]() ,交
,交![]() 轴于点
轴于点![]() ,使得线段
,使得线段![]() 被点
被点![]() ,
, ![]() 三等分,求直线
三等分,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟) |
|
|
|
|
|
次数 | 8 | 14 | 8 | 8 | 2 |
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为![]() 分钟.
分钟.
(Ⅰ)若李先生上.下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设![]() 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)写出函数![]() 的值域,单调区间(不必证明);
的值域,单调区间(不必证明);
(2)是否存在实数![]() 使得
使得![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点![]() ,且在
,且在![]() 轴上截得的弦长为4,记动圆圆心的轨迹为曲线C.
轴上截得的弦长为4,记动圆圆心的轨迹为曲线C.
(Ⅰ)求直线![]() 与曲线C围成的区域面积;
与曲线C围成的区域面积;
(Ⅱ)点![]() 在直线
在直线![]() 上,点
上,点![]() ,过点
,过点![]() 作曲线C的切线
作曲线C的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,直线
轴非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程及直线
的极坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com