
【题目】已知函数![]() ,
, ![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ)讨论函数![]() 的极值点的个数;
的极值点的个数;
(Ⅱ)若函数![]() 的图象与函数
的图象与函数![]() 的图象有两个不同的交点,求实数
的图象有两个不同的交点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)详见解析; (Ⅱ)![]() .
.
【解析】试题分析:(1)对函数![]() 进行求导,根据基本不等式得出
进行求导,根据基本不等式得出![]() 的范围,按照
的范围,按照![]() 的最小值是否在定义域内分两类讨论,: ①当
的最小值是否在定义域内分两类讨论,: ①当![]() ,
, ![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 没有极值点;②当
没有极值点;②当![]() ,转化为方程
,转化为方程![]() 正数解的个数;(2) 函数
正数解的个数;(2) 函数![]() 的图象与函数
的图象与函数![]() 的图象有两个不同的交点,转化为
的图象有两个不同的交点,转化为![]() 由两个不同的根,通过参变分离,构造新的函数,求导判断单调性与最值,求出参数的范围.
由两个不同的根,通过参变分离,构造新的函数,求导判断单调性与最值,求出参数的范围.
试题解析:(Ⅰ)![]() ,
,
∵![]() ,∴
,∴![]() ,
,
①当![]() ,即
,即![]() 时,
时, ![]() 对
对![]() 恒成立,
恒成立, ![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 没有极值点;
没有极值点;
②当![]() ,即
,即![]() 时,方程
时,方程![]() 有两个不等正数解
有两个不等正数解![]() ,
, ![]() ,
,
![]() ,
,
不妨设![]() ,则当
,则当![]() 时,
时, ![]() ,
, ![]() 为增函数;当
为增函数;当![]() 时,
时, ![]() ,
, ![]() 为减函数;
为减函数; ![]() 时,
时, ![]() ,
, ![]() 为增函数,所以
为增函数,所以![]() ,
, ![]() 分别为
分别为![]() 极大值点和极小值点,即
极大值点和极小值点,即![]() 有两个极值点.
有两个极值点.
综上所述,当![]() 时,
时, ![]() 没有极值点;当
没有极值点;当![]() 时,
时, ![]() 有两个极值点.
有两个极值点.
(Ⅱ)令![]() ,得
,得![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
令![]() (
(![]() ),
),
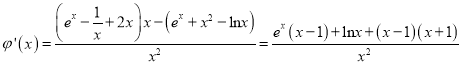 ,
,
∵![]() ,∴
,∴![]() 时,
时, ![]() ,
, ![]() 为减函数;
为减函数;
![]() 时,
时, ![]() ,
, ![]() 为增函数,∴
为增函数,∴![]() ,
,
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∵函数![]() 图象与函数
图象与函数![]() 图象有两个不同交点,∴实数
图象有两个不同交点,∴实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是 . (填序号)
①若集合A={x|kx2+4x+4=0}中只有一个元素,则k=1;
②在同一平面直角坐标系中,y=2x与y=2﹣x的图象关于y轴对称;
③y=( ![]() )﹣x是增函数;
)﹣x是增函数;
④定义在R上的奇函数f(x)有f(x)f(﹣x)≤0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x<0时,f(x)=( ![]() )x .
)x .
(1)求当x>0时f(x)的解析式;
(2)画出函数f(x)在R上的图象; 
(3)写出它的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个命题p:x∈R,sinx+cosx>m恒成立,q:x∈R,y=(2m2﹣m)x为增函数.若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 与
与 ![]() 为互相垂直的单位向量,
为互相垂直的单位向量, ![]() ,
, ![]() 且
且 ![]() 与
与 ![]() 的夹角为锐角,则实数λ的取值范围是( )
的夹角为锐角,则实数λ的取值范围是( )
A.(﹣∞,﹣2) ![]()
B.( ![]() ,+∞)
,+∞)
C.(﹣2, ![]() )
) ![]()
D.(﹣ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com