
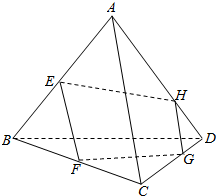
 如图,ABCD为空间四边形,点E,F分别是AB,BC的中点,点G,H分别在CD,AD上,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$CD.
如图,ABCD为空间四边形,点E,F分别是AB,BC的中点,点G,H分别在CD,AD上,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$CD.分析 (1)由已知推导出EF∥AC,EF=$\frac{1}{2}$AC,HG∥AC,HG=$\frac{1}{3}$AC,由此得到四边形EFGH的形状为梯形,
(2)EH和FG为梯形的两腰,从而EH和FG必交于一点,设交点为Q,再推导出Q∈BD,由此能证明EH,FG和BD三线交于点Q.
解答 解:(1)∵E,F分别是AB,BC的中点 ,
,
∴EF∥AC,EF=$\frac{1}{2}$AC,
∵点G,H分别在CD,AD上,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$CD,
∴△HGD∽△ACD,
∴HG∥AC,HG=$\frac{1}{3}$AC,
∴EF∥HG,EF≠HG,
四边形EFGH的形状为梯形,
证明:(2)∵EH和FG为梯形EFGH的两腰,
∴EH和FG必交于一点,设交点为Q,
∵Q∈EH,EH?平面ABD,Q∈FG,FG?平面BCD,
∴Q∈平面ABD,Q∈平面BCD,
∵面ABD∩面BCD=BD,∴Q∈BD,
∴EH,FG和BD三线交于点Q.
点评 本题考查四边形形状的判断,考查三线交于一点的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径$r=\root{3}{10}$毫米,滴管内液体忽略不计.如果瓶内的药液恰好156分钟滴完,则每分钟应滴下75滴.
如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径$r=\root{3}{10}$毫米,滴管内液体忽略不计.如果瓶内的药液恰好156分钟滴完,则每分钟应滴下75滴.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com