
【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明: ![]() 为等比数列.
为等比数列.
【答案】(1) ![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(1)由题意令![]() ,把数列的和用项的形式列出,代入已知求出
,把数列的和用项的形式列出,代入已知求出![]() ;(2)由已知拆项,化简为数列的递推关系式形式,由等比数列的定义以及
;(2)由已知拆项,化简为数列的递推关系式形式,由等比数列的定义以及![]() 代入,即可证明.
代入,即可证明.
试题解析:
(1)解:当n=2时,4S4+5S2=8S3+S1,即4![]() +5
+5![]() =8
=8![]() +1,解得a4=
+1,解得a4=![]() .
.
(2)证明:由4Sn+2+5Sn=8Sn+1+Sn-1(n≥2),得4Sn+2-4Sn+1+Sn-Sn-1=4Sn+1-4Sn(n≥2),即4an+2+an=4an+1(n≥2).
因为 4a3+a1=4×![]() +1=6=4a2,
+1=6=4a2,
所以 4an+2+an=4an+1,
所以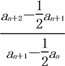 =
=![]() =
=![]() =
=
![]() =
=![]() ,
,
所以 数列![]() 是以a2-
是以a2-![]() a1=1为首项,
a1=1为首项,![]() 为公比的等比数列.
为公比的等比数列.
点睛: 等比数列的判断方法有:(1)定义法:若![]() (
(![]() 为非零常数)或
为非零常数)或![]() (
(![]() 为非零常数且
为非零常数且![]() 且
且![]() ),则
),则![]() 是等比数列.(2)中项公式法:在数列
是等比数列.(2)中项公式法:在数列![]() 中,
中, ![]() 且
且![]() (
(![]() ),则数列
),则数列![]() 是等比数列.(3)通项公式法:若数列通项公式可写成
是等比数列.(3)通项公式法:若数列通项公式可写成![]() (
(![]() ,
, ![]() 均是不为0的常数,
均是不为0的常数, ![]() ),则
),则![]() 是等比数列.
是等比数列.


科目:高中数学 来源: 题型:
【题目】如图,点![]() 是椭圆
是椭圆![]() 的一个顶点,
的一个顶点, ![]() 的长轴是圆
的长轴是圆![]() 的直径.
的直径. ![]() 是过点
是过点![]() 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中![]() 交圆
交圆![]() 于两点
于两点![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 面积取最大值时直线
面积取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,数列
,数列![]() 满足
满足![]() 点
点![]() 在直线
在直线![]() 上.
上.
(1)求数列![]() ,
, ![]() 的通项
的通项![]() ,
, ![]() ;
;
(2)令![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() ,求对所有的正整数
,求对所有的正整数![]() 都有
都有![]() 成立的
成立的![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一袋中装有6个黑球,4个白球.如果不放回地依次取出2个球.求:
(1)第1次取到黑球的概率;
(2)第1次和第2次都取到黑球的概率;
(3)在第1次取到黑球的条件下,第2次又取到黑球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,ABCD﹣A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1 , B1C1的中点,P是上底面的棱AD上的一点,AP= ![]() ,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= .
,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= . 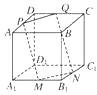
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn,已知a1=10,a2为整数,且Sn≤S4.
(1)求{an}的通项公式;
(2)设bn=![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 为非零常数.
为非零常数.
(1)若![]() ,
, ![]() ,求证:
,求证: ![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 是公差不等于零的等差数列.
是公差不等于零的等差数列.
①求实数![]() ,
, ![]() 的值;
的值;
②数列![]() 的前
的前![]() 项和
项和![]() 构成数列
构成数列![]() ,从
,从![]() 中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为
中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为![]() 的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由.
的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双“十一”结束之后,某网站针对购物情况进行了调查,参与调查的人主要集中在[20,50]岁之间,若规定:购物600(含600元)以下者,称为“理智购物”,购物超过600元者被网友形象的称为“剁手党”,得到如下统计表:
分组编号 | 年龄分组 | 球迷 | 所占比例 |
1 | [20,25) | 1000 | 0.5 |
2 | [25,30) | 1800 | 0.6 |
3 | [30,35) | 1200 | 0.5 |
4 | [35,40) | a | 0.4 |
5 | [40,45) | 300 | 0.2 |
6 | [45,50] | 200 | 0.1 |
若参与调查的“理智购物”总人数为7720人.
(1)求a的值;
(2)从年龄在[20,35)的“剁手党”中按照年龄区间分层抽样的方法抽取20人; ①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率;
②从这20人中随机抽取2人,用ζ表示年龄在[20,25)之间的人数,求ξ的分布列及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}的前n项和为Sn, S3=a4+6,且a1, a4, a13成等比数列.
(1)求数列{an}的通项公式;
(2)设![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com