Question

7．在平面直角坐标系中，设点P₁（x₁，y₁）、P₂（x₂，y₂），称d（P₁，P₂）=max{|x₁-x₂|，|y₁-y₂|}（其中max{a，b}表示a、b中的较大数）为P₁、P₂两点的“切比雪夫距离”；
（1）若P（3，1）、Q为直线y=2x-1上的动点，求P，Q两点的“切比雪夫距离”的最小值；
（2）定点C（x₀，y₀），动点P（x，y）满足d（C，P）=r（r＞0），请求出P点所在的曲线所围成图形的面积．

Answer 1

分析 （1）设Q（x，2x-1），可得d（P，Q）=max{|x-3|，|2-2x|}，讨论|x-3|，|2-2x|的大小，可得距离d，再由函数的性质，可得最小值；
（2）运用分段函数的形式求得d（C，P），分析各段与不等式表示的区域的图形，即可得到面积．

解答 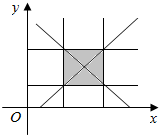解：（1）设Q（x，2x-1），可得d（P，Q）=max{|x-3|，|2-2x|}，
由|x-3|≥|2-2x|，解得-1≤x≤$\frac{5}{3}$，即有d（P，Q）=|x-3|，
当x=$\frac{5}{3}$时，取得最小值$\frac{4}{3}$；
由|x-3|＜|2-2x|，解得x＞$\frac{5}{3}$或x＜-1，即有d（P，Q）=|2x-2|，
d（P，Q）的范围是（3，+∞）∪（$\frac{4}{3}$，+∞）=（$\frac{4}{3}$，+∞）．
综上可得，P，Q两点的“切比雪夫距离”的最小值为$\frac{4}{3}$；
（2）由题意可得，d（C，P）=r=$\left\{\begin{array}{l}{|{x}_{0}-x|，|{x}_{0}-x|≥|{y}_{0}-y|}\\{|{y}_{0}-y|，|{x}_{0}-x|＜|{y}_{0}-y|}\end{array}\right.$，
当|x₀-x|≥|y₀-y|，|x₀-x|=r，即有x=x₀±r，
围成的图形为关于点（x₀，y₀）对称的三角形区域；
当|x₀-x|＜|y₀-y|，|y₀-y|=r，即有y=y₀±r，
围成的图形为关于点（x₀，y₀）对称的三角形区域．
综上可得P点所在的曲线所围成图形为边长为2r的正方形区域，
其面积为4r²．

点评 本题考查新定义的理解和运用，考查不等式的解法和平面区域的面积求法，注意运用分类讨论的思想方法，考查运算能力，属于中档题．