
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)证明:![]() //平面
//平面![]() ;
;
(2)设![]() ,三棱锥
,三棱锥![]() 的体积
的体积![]() ,求
,求![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)详见解析(2) ![]()
【解析】
试题分析:(1)连结BD、AC相交于O,连结OE,则PB∥OE,由此能证明PB∥平面ACE.(2)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出A到平面PBD的距离
试题解析:(I)设BD交AC于点O,连结EO。
因为ABCD为矩形,所以O为BD的中点。
又E为PD的中点,所以EO∥PB
又EO![]() 平面AEC,PB
平面AEC,PB![]() 平面AEC
平面AEC
所以PB∥平面AEC。
(II)![]()
由![]() ,可得
,可得![]() .
.
作![]() 交
交![]() 于
于![]() 。
。
由题设易知![]() ,所以
,所以![]()
故![]() ,
,
又![]() 所以
所以![]() 到平面
到平面![]() 的距离为
的距离为![]()
法2:等体积法
![]()
由![]() ,可得
,可得![]() .
.
由题设易知![]() ,得BC
,得BC![]()
假设![]() 到平面
到平面![]() 的距离为d,
的距离为d,
又因为PB=![]()
所以![]()
又因为![]() (或
(或![]() ),
),
![]() ,
,
所以![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinωxcosωx+2![]() sin2ωx﹣
sin2ωx﹣![]() (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求函数f(x)的单调增区间;
(2)将函数f(x)的图象向左平移![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,△PAB是正三角形,四边形ABCD是矩形,且平面PAB⊥平面ABCD,PA=2,PC=4.

(Ⅰ)若点E是PC的中点,求证:PA∥平面BDE;
(Ⅱ)若点F在线段PA上,且FA=λPA,当三棱锥B﹣AFD的体积为![]() 时,求实数λ的值.
时,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在△ABC中,a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,在四面体PABC中,S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.写出对四面体性质的猜想,并证明你的结论
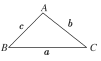

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两煤矿每年的产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地,东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.要使总运费最少,煤矿应怎样编制调运方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数据![]() 是郑州市普通职工
是郑州市普通职工![]() 个人的年收入,若这
个人的年收入,若这![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A. 年收入平均数大大增大,中位数一定变大,方差可能不变
B. 年收入平均数大大增大,中位数可能不变,方差变大
C. 年收入平均数大大增大,中位数可能不变,方差也不变
D. 年收入平均数可能不变,中位数可能不变,方差可能不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com