
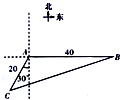
 如图,位于A处的海面观测站获悉,在其正东方向相距40海里的B处有一艘渔船遇险,并在原地等待营救.在A处南偏西30°且相距20海里的C处有一艘救援船,该船接到观测站通告后立即前往B处求助,则sin∠ACB=$\frac{\sqrt{21}}{7}$.
如图,位于A处的海面观测站获悉,在其正东方向相距40海里的B处有一艘渔船遇险,并在原地等待营救.在A处南偏西30°且相距20海里的C处有一艘救援船,该船接到观测站通告后立即前往B处求助,则sin∠ACB=$\frac{\sqrt{21}}{7}$. 科目:高中数学 来源: 题型:解答题
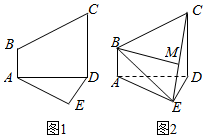 已知五边形ABCDE由直角梯形ABCD与直角△ADE构成,如图1所示,AE⊥DE,AB∥CD,AB⊥AD,且AD=CD=2DE=3AB,将梯形ABCD沿着AD折起,形成如图2所示的几何体,且使平面ABCD⊥平面ADE.
已知五边形ABCDE由直角梯形ABCD与直角△ADE构成,如图1所示,AE⊥DE,AB∥CD,AB⊥AD,且AD=CD=2DE=3AB,将梯形ABCD沿着AD折起,形成如图2所示的几何体,且使平面ABCD⊥平面ADE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com