Question

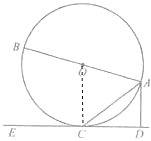
【题目】如图，已知AB是⊙O的直径，AC是弦，AD⊥CE，垂足为D，AC平分∠BAD．

（1）求证：直线CE是⊙O的切线；
（2）求证：AC2=ABAD．

Answer 1

【答案】
（1）证明：连接OC，如下图所示：

因为OA=OC，

所以∠OCA=∠OAC．

又因为AD⊥CE，

所以∠ACD+∠CAD=90°，

又因为AC平分∠BAD，

所以∠OCA=∠CAD，

所以∠OCA+∠CAD=90°，

即OC⊥CE，

所以CE是⊙O的切线．

（2）证明：连接BC，

因为AB是⊙O的直径，

所以∠BCA=∠ADC=90°，

因为CE是⊙O的切线，

所以∠B=∠ACD，

所以△ABC∽△ACD，

所以 ，

即AC2=ABAD．

【解析】（1）连接OC，利用△OAC为等腰三角形，结合同角的余角相等，我们易结合AD⊥CE，得到OC⊥DE，根据切线的判定定理，我们易得到结论；（2）连接BC，我们易证明△ABC∽△ACD，然后相似三角形性质，相似三角形对应边成比例，易得到结论．