
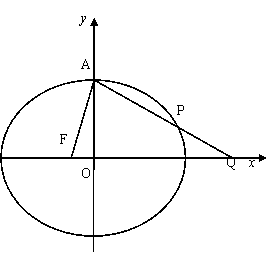
(08年扬州中学) 设椭圆C:![]() 的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且![]() .
.
⑴求椭圆C的离心率;⑵若过A、Q、F三点的圆恰好与直线l:![]() 相切,求椭圆C的方程.
相切,求椭圆C的方程.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(08年扬州中学) 已知数列![]() ,
,![]() 中,
中,![]() ,且
,且![]() 是函数
是函数
![]() 的一个极值点.
的一个极值点.
(1)求数列![]() 的通项公式;
的通项公式;
(2) 若点![]() 的坐标为(1,
的坐标为(1,![]() )(
)(![]() ,过函数
,过函数![]() 图像上的点
图像上的点![]() 的切线始终与
的切线始终与![]() 平行(O 为原点),求证:当
平行(O 为原点),求证:当![]() 时,不等式
时,不等式
![]() 对任意
对任意![]() 都成立.
都成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年扬州中学) (16分)
用![]() 表示数列
表示数列![]() 从第
从第![]() 项到第
项到第![]() 项(共
项(共![]() 项)之和.
项)之和.
(1)在递增数列![]() 中,
中,![]() 与
与![]() 是关于
是关于![]() 的方程
的方程![]() (
(![]() 为正整数)的两个根.求
为正整数)的两个根.求![]() 的通项公式并证明
的通项公式并证明![]() 是等差数列;
是等差数列;
(2)对(1)中的数列![]() ,判断数列
,判断数列![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的类型;
的类型;
(3)对一般的首项为![]() ,公差为
,公差为![]() 的等差数列,提出与(2)类似的问题,你可以得到怎样的结论,证明你的结论.
的等差数列,提出与(2)类似的问题,你可以得到怎样的结论,证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com