
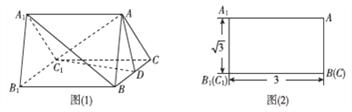
【题目】如图(1)是一个水平放置的正三棱柱![]() ,
, ![]() 是棱
是棱![]() 的中点,正三棱柱的主视图如图(2).
的中点,正三棱柱的主视图如图(2).
(1)图(1)中垂直于平面![]() 的平面有哪几个(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个(直接写出符合要求的平面即可,不必说明或证明)
(2)求正三棱柱![]() 的体积;
的体积;
(3)证明: ![]() 平面
平面![]() .
.
科目:高中数学 来源: 题型:
【题目】现有一张长为![]() ,宽为
,宽为![]() (
(![]() )的长方形铁皮
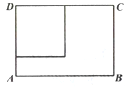
)的长方形铁皮![]() ,准备用它做成一个无盖长方体铁皮容器,要求材料利用率为100%,不考虑焊接处损失.如图,在长方形
,准备用它做成一个无盖长方体铁皮容器,要求材料利用率为100%,不考虑焊接处损失.如图,在长方形![]() 的一个角上剪下一块边长为
的一个角上剪下一块边长为![]() 的正方形铁皮,作为铁皮容器的底面,用余下材料剪拼后作为铁皮容器的侧面,设长方体的高为
的正方形铁皮,作为铁皮容器的底面,用余下材料剪拼后作为铁皮容器的侧面,设长方体的高为![]() ,体积为
,体积为![]() .
.
(Ⅰ)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)求该铁皮容器体积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的方程是
的方程是![]() ,圆
,圆![]() 的参数方程是
的参数方程是![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)分别求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() (其中
(其中![]() )与圆
)与圆![]() 交于
交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,射线
,射线![]() 与圆
与圆![]() 交于
交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的月固定成本为10(万元),每生产![]() 件,需另投入成本为
件,需另投入成本为![]() (万元).当月产量不足30件时,
(万元).当月产量不足30件时, ![]() (万元);当月产量不低于30件时,
(万元);当月产量不低于30件时, ![]() (万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.
(万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.
(1)写出月利润![]() (万元)关于月产量
(万元)关于月产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)当月产量为多少件时,该厂所获月利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子显露显性特征的概率是多少?
(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四个命题:
①在回归分析中, ![]() 可以用来刻画回归效果,
可以用来刻画回归效果, ![]() 的值越大,模型的拟合效果越好;
的值越大,模型的拟合效果越好;
②在独立性检验中,随机变量![]() 的值越大,说明两个分类变量有关系的可能性越大;
的值越大,说明两个分类变量有关系的可能性越大;
③在回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均增加1个单位;
平均增加1个单位;
④两个随机变量相关性越弱,则相关系数的绝对值越接近于1;
其中真命题是:
A. ①④ B. ②④ C. ①② D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com