
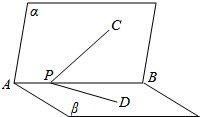
 如图,平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,则∠CPD=60°.
如图,平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,则∠CPD=60°. 分析 作CO⊥AB,交AB于O,在平面β内作OD⊥AB,交PD于点D,连结CD,由已知推导出△COP,△DOP,△COD是全等的等腰直角三角形,由此能求出∠CPD.
解答  解:作CO⊥AB,交AB于O,在平面β内作OD⊥AB,交PD于点D,连结CD,
解:作CO⊥AB,交AB于O,在平面β内作OD⊥AB,交PD于点D,连结CD,
∵平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,
∴∠COD是二面角α-AB-β的平面角,∴∠COD=90°,
∴△COP,△DOP,△COD是全等的等腰直角三角形,
∴PC=PD=CD,
∴∠CPD=60°.
故答案为:60°.
点评 本题考查角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | {x|-3<x<0} | B. | {x|-1≤x<0} | C. | {x|x<-1} | D. | {x|-1<x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在直三棱柱ABC-A1B1C1中,AC=4,CB=AA1=2,AB=2$\sqrt{3}$ E,F,G分别是A1C1,BC,AA1的中点.
在直三棱柱ABC-A1B1C1中,AC=4,CB=AA1=2,AB=2$\sqrt{3}$ E,F,G分别是A1C1,BC,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产品名称:180克维达卫生纸 |
| 产品编号:v4131 |
| 主要原料:100%原生木浆 |
| 执行标准:GB20810 优等品(合格) |
| 生产日期:见包装 保质期:三年 |
| 规格:3层 138mm×104mm/节 净含量:180克 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com