
【题目】函数 ![]() 是偶函数,求解下列问题.
是偶函数,求解下列问题.
(1)求θ;
(2)将函数y=f(x)的图象先纵坐标不变,横坐标缩短为原来的 ![]() 倍,再向左平移
倍,再向左平移 ![]() 个单位,然后向上平移1个单位得到y=g(x)的图象,若关于x的方程
个单位,然后向上平移1个单位得到y=g(x)的图象,若关于x的方程 ![]() 在
在 ![]() 有且只有两个不同的根,求m的范围.
有且只有两个不同的根,求m的范围.
【答案】
(1)
解: ,
而f(x)为偶函数,则 即
∴ ![]() ,k∈Z
,k∈Z
又∵ ,∴
(2)
解:f(x)=2cos2x,
∴ 可化为 与 在
1<m≤2或﹣2≤m<﹣1
【解析】分析:(1)先用辅助角法将函数转化为一个角的一种三角函数,再由其为偶函数求解.(2)由(1)知f(x)然后严格按照变换要求得到g(x),再将方程 ![]() 转化为
转化为 ![]() 求解.
求解.
【考点精析】关于本题考查的函数y=Asin(ωx+φ)的图象变换,需要了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能得出正确答案.
的图象才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来发展的新机遇,2016年双11期间,某购物平台的销售业
绩高达1207亿人民币。与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.9,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为140次.
(1)请完成下表,并判断是否可以在犯错误概率不超过0.5%的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量![]() :
:
①求对商品和服务全好评的次数![]() 的分布列;
的分布列;
②求![]() 的数学期望和方差.
的数学期望和方差.

( ,其中
,其中![]() )
)
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 140 | ||
对商品不满意 | 10 | ||
合计 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在冬季供暖时减少能量损耗,房屋的屋顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:
(单位:![]() )满足关系:
)满足关系:![]() ,若不建隔热层,每年能源消耗费用为8万元,设
,若不建隔热层,每年能源消耗费用为8万元,设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:①y= ![]() 是奇函数;
是奇函数;
②若α,β是第一象限角,且α>β,则cosα<cosβ;
③函数f(x)=2x﹣x2在R上有3个零点;
④函数y=sin2x的图象向左平移 ![]() 个单位,得到函数
个单位,得到函数 ![]() 的图象.
的图象.
其中正确命题的序号是 . (把正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,A(a,0),B(0,b),O(0,0),△OAB的面积为1.
,A(a,0),B(0,b),O(0,0),△OAB的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P是椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N.求证:|AN||BM|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个圆形波浪实验水池的中心有三个振动源,假如不计其它因素,在t秒内,它们引发的水面波动可分别由函数 ![]() 和
和 ![]() 描述,如果两个振动源同时启动,则水面波动由两个函数的和表达,在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现的状态是( )
描述,如果两个振动源同时启动,则水面波动由两个函数的和表达,在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现的状态是( )
A.仍保持平静
B.不断波动
C.周期性保持平静
D.周期性保持波动
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体ABCD﹣A1B1C1D1 , O是底ABCD对角线的交点.求证: 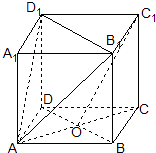
(1)C1O∥面AB1D1;
(2)面BDC1∥面AB1D1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com