练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】命题p：关于x的方程x2＋ax＋2＝0无实根，命题q：函数f(x)＝logax在(0，＋∞)上单调递增，若“p∧q”为假命题，“p∨q”真命题，求实数a的取值范围

    【答案】(－2，1]∪[2，＋∞)

    【解析】

    试题分析：首先判断命题p,q为真命题时的对应的a的取值范围，由“p∧q”为假命题，“p∨q”真命题可知两命题一真一假，分两种情况讨论可求得a的取值范围

    试题解析：∵方程x2＋ax＋2＝0无实根，

    ∴△＝a2－8<0，∴－2<a<2，∴p：－2<a<2.

    ∵函数f(x)＝logax在(0，＋∞)上单调递增，∴a>1.

    ∴q：a>1.∵p∧q为假，p∨q为真，∴p与q一真一假．

    当p真q假时，－2<a≤1，当p假q真时，a≥2.

    综上可知，实数a的取值范围为(－2，1]∪[2，＋∞)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知{an}是一个公差为d（d≠0）的等差数列，它的前10项和S10=110，且a1，a2，a4成等比数列。

    （1）证明：a1=d；

    （2）求公差d的值和数列{an}的通项公式。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是不同的直线， 是不同的平面，已知，下列说法正确的是 （ ）

    A. 若，则 B. 若，则

    C. 若，则 D. 若，则

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的焦距为2，离心率为，轴上一点的坐标为．

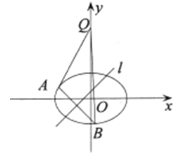
    （Ⅰ）求该椭圆的方程；

    （Ⅱ）若对于直线，椭圆上总存在不同的两点与关于直线对称，且,求

    实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD是正方形，延长CD至E，使得DE＝CD.若动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，其下列叙述正确的是（ ）

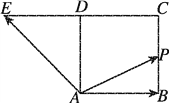
    A. 满足λ＋μ＝2的点P必为BC的中点

    B. 满足λ＋μ＝1的点P有且只有一个

    C. λ＋μ的最大值为3

    D. λ＋μ的最小值不存在

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且acosC+ccosA=2bcosA．
    （1）求角A的值；
    （2）若, ，求△ABC的面积S．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知两直线l1：ax﹣by+4=0，l2：（a﹣1）x+y+b=0，分别求满足下列条件的a，b值

    （1）l1⊥l2，且直线l1过点（﹣3，﹣1）；

    （2）l1∥l2，且直线l1在两坐标轴上的截距相等．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知长方形中，为的中点，将 沿折起，使得平面平面．

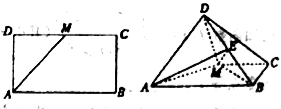
    （1）求证：；

    （2）若点是线段上的一动点，问点在何位置时，三棱锥的体积与四棱锥的体积之比为1：3？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前n项和为Sn，且首项a1≠3，an＋1＝Sn＋3n（n∈N*）．

    （1）求证：数列{Sn－3n}是等比数列；

    （2）若{an}为递增数列，求a1的取值范围．

    查看答案和解析>>

    同步练习册答案